수학중독 | 음수의 제곱근
본문
※ 영상을 선명하게 보기 안내
- 유튜브 영상에서 오른쪽하단에 톱니바퀴를 클릭합니다.
- 팝업목록에서 "품질" 선택하세요.
- 원하는 해상도를 선택해주세요.
※ 모바일에서 Wifi가 아니라면 데이타가 소진될 수 있으니 주의바랍니다.
수학중독님의 중학교수학강의 청각장애인을 위한 자막
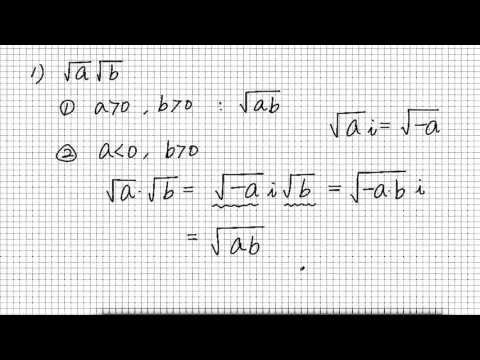
음수의 제곱근의 대해서 알아봅시다 자 우리가 이미 알고 있는 것은 이 허
수단이가 - 일에 노트가 - 일이다 라는 것을 정의로부터 알고 있는
상황입니다
요걸 이제 일반적인 케이스 로 확장해 보자 하는게 이 금세 제곱근 이에요
자 먼저 이 얘기를 하기에 앞서 우리가 그 루트 5 라는 것의 의미를
한번 봅시다
만약에 우리가 x 간호 듀오 라는 것은 어떻게 생각할 수 있냐면
x 를 두번 곱해 쓸 때 5가 된다는 겁니다 즉 거꾸로 말하면 이 루트
오라는 놈은 2번 곱해서 5가 되는 수를 이런 기호로 나타내자 라고
우리가 약속을 한 거죠
즉 x 의 제곱은 루트 오게 제곱이 다 이렇게 쓸 수가 있는 거구요
따라서 예를 넘겨서 인수 분해를 하면 x 제곱 빼기 제곱이 되는거니까
한번에 갈게요
한번은 + 그 다음에 한번은 - 이렇게 돼서 뭐가 됨과 결국 x 는 플라
스마 인 어스 루트 오다 라는 것을 얻어낼 수가 있는 겁니다
즉 이 경우 x 가 2개가 나오긴 하지만 여기서 우리가 누트 오다 라는
것은 여기서 나오는 두 개의 의 값 중에 양수인 것을 우리가 루츠 오라고
하자 라는 거죠
그처럼 자 그렇다면 봐
우리가 예를 들어서 루트에 - 5 라는 것을 어떻게 생각해 볼 수 있느냐
라는 겁니다
이 노트에 - 오는 요거랑 구별하게 색깔을 바꿔 볼게요 결국 어떤 것을
2번 곱해 쓸 때 - 5가 되는 이러한 x 를 의미하는 걸 거구요
이것을 다시 쓰게 되면 우리는 x 의 제곱 이라는 놈이 결국은 잘 가 요
오라는 법은 요우 츄오 를 의미 하면 무 쭈웁 의 제곱과 - 이라는 놈은
아이의 제 곡 요렇게 쓸 수 있는 거 아니겠냐 라는 거죠
이거를 다시 표현하면 x 의 제곱은 무 쭈웁 곱하기 아이의 전체의 의
제곱 이다
요렇게 표현할 수가 있게 되는 겁니다 그럼 결과적으로 똑같이 우리는 x
는 여기에서 와 똑같죠
플라 스마 인 어스 루트 o 아이를 얻게 되는데 이 롬에 앞쪽에 그저
물론 이거는 파스 야 - 냐를 허수 에서는 부어오를 논 하긴 좀
그렇습니다
그저 에 따라서 방학 그냥 허수 부의 부가 플러스 냐 허수 부의 부가 -
냐 이렇게 얘기를 해야지
이수 자체가 양수 냐 음순 야 이렇게 얘기하면 안 됩니다 알겠죠
따라서 방 이 커 스 부 의 부가 양수인 노블 우리가 루트에 - 오다
이렇게 표현했기 때문에 따라서 팔아 루트에 oi 라는 놈이 결과적으로는
루트에 - o 와 똑같다고 말을 할 수가 있는 겁니다
이해가 됩니까 그래서 여러분이 기억해야 될 건 딱 이거 하나에요 이거
하나
오케이 어 그래서 일반적으로 얘기를 하자면 우리가 어떤 얘기를 할 수가
있냐면 팝
a 가 양수 일대 루트에 - a 라는 놈은
결국 채고 끈 안에 음수가 들어간 켜 있으나
따라서 얘는 다시 쓰면 루트에 a 에
아이다 이렇게 쓸 수가 있는 거고 얘는 그냥 우리가 알고 있는 데로 하면
요렇게 쓸 수가 있게 된 겁니다 왜 아이가 루트에 - 1과 똑같은 높
이기 때문에
됐습니까 예 그래서 요런 식으로 쓴다 라는 요 것만 여러분이 잘 알고
있으면 된다는 거예요
백조 그래서 요거 5 기억해 주시기 바랍니다
그럼 1 우리가 이제 뭘 배워 거냐면 2
음수 의 제곱근 와 관련된
섬 지를 배울 겁니다 근데 요게 또 시험에 잊을만하면 한 번씩 나오는
거에요
달마 우리가 지금 합격 때 몰 베어 냐 면
a 도 0보다 크고 비도 0보다 클 때
루트 a 루트 b 라는 놈은 그냥 루트에 a b 가 된다 라는 걸
배웠어요
뭐 혹은 루트에 a 제곱 2가 되면
이재 것만 밖으로 나와서 a 루트 삐 다 이러한 성질들을 배웠죠
뭐 아니면 루트 b 분의 루트 a 는 그저 예 루트에 비부 에이다 꽃
이진은 루트에
빚에 고픈 a 라는 놈은 그냥 b 분의 누트 a 와 같다 라는 요러한
성질들을 우리가 중학교때 있는 배웠습니다
자 그때 관심을 가져야 될 것은 바로 뭐예요
a 와 b 까 모두다 0보다 클 때 이러한 성질들을 갖는 다는 거지 근데
이제 우리가 이 누트 안의 값이 0보다 작은 케이스에 대해서 배워 딴
말이야 음색에 복근
그러면 이러한 연산 들의 혹시 a 나 b 가 음수가 돼 버리면 어떻게
동작할 건가
고고 를 번 시간에 배운 다는 거죠 자 그럼 바 다소 헷갈릴 수 있으므로
정신 바짝 차리고 봅니다
우리가 첫 번째 이 알아야 될게 루트 a 루트 삐삐가 뭐가 될까 를
배워야 되요
당연히 1번 a 가 0보다 크고 b 가 0보다 큰 경우라면 이름은 그냥
루트 a b 가 된다는 걸 중학교때 배웠고 요
우리가 봐야 될거 두번째꺼 둘중에 하나만 0보다 작은 케이스를 한번
생각해보자 이가
그러면 a 가 음수 고삐가 양수인 상황에서 루트 a 곱하기 루트 삐 라는
놈은 어떻게 되냐면 잘 밤 여러분 우리 배운 바에 의하면 이걸 이렇게 그
집어 낼 수가 있죠
정치 바짝 차례 대해 a 가 음수 기 때문에 루트에 이라는 몸은 음수의
제곱근 이 된거고
우리가 배운 바에 의해서 여기를 양수로 만들어주고 줘 - 있는 양수 및
아 그 다음에 루트 쉬어주고 아이를 밖으로 빼냈다 이렇게 생각하시면 되요
그쵸 쉽게 말하면 루트에 a 라는 놈은 누
트에 - ai 요 제곱 욕이 되는 거잖아
그 직 그러나 이제 번만 밖으로 빼 내면 되니까
결과적으로 뭐가 된 거야 루트에 마이너스의 아이와 가 딱 이렇게 볼 수가
있는 겁니다
우리 위에서 배우가 위에서 됐지 자 그럼 하라
이제 얘도 양수 고 요놈도 양의 제곱근 요것도 양수의 제곱근 인건 아니까
이둘은 간단하게 그냥 루트에 요 위에 거 1번 사용 하면 되잖아 그럼 -
a 와 b 의 곡으로 만들수가 있고 뒤에 아이가 붙음 됩니다
자 그런데 우리가 몰 배웠어 이 라는 놈은 이 루트의 ai 라는
목은 결국 루트에 - a 와 똑같다는 걸 알고 있잖아
그제 그럼 아이가 루트 안으로 들어오면서 다시 뭘 만들기 때문에 - 2
를 만들기 때문에 결국에는 ad 가 된다 라는 걸 볼 수가 있죠
음 그래서 방 a 가 0 보다 짧고 b 가 0보다 크
둘중에 하나만 음수 일때도 루트 2 곱하기 노트 삐는 루트 a b 가
됩니다
자 그런데 잘 봐라 세번째
둘다 0보다 작은 어떻게 될 거야 음 둘다 이보다 짧을 때는 잘바 루트
a 루트 b 라는 놈은
똑같이 쓸겁니다 요 놈의 아이 곱하기 루트 - 비에 아이가 되는데
ii 가 두번 곱해 줬으니까 이름은 그냥 - 일이 되는거구요 예 그럼
요렇게 써볼까 루트에 - a 그 나무 트에 - b 곱하기 - 2d ii
에 제 법이니까
근데 지금 - a - b 는 모두 양수 이기 때문에 얘네들은 우리가 1
즉 중학교 때 배운 것에 의해서 그냥 루트에 - a 와 - b 를 곱한
다음에 요렇게 써 줄 수가 있구요
결국 얘는 뭐가 되냐 하면 요법을 - 로 앞으로 빼내면 루트에 요렇게
고파 가짜 ab 된걸 볼 수가 있습니다
자 여러분들 기억하세요 이거 되게 중요합니다 잘바 어
둘다 0보다 작을 때에 루트 a 와 루트 b 를 곱한 것은
- 가 앞으로 나오면서 루트 a b 가 된다는 겁니다 자 중요한 건 누구
양 바로 2 - 입니다 - 이거 꼭 기억하셔야 되요
그래서 여러분이 알아야 될 건 뭐냐면 아 결국 바 루트 a 루트 삐삐가
다 루트 a b 가 되는데
딱 한 가지 경우 즉 a 가 0 보다 작고 비도 0보다 짝은 이 경우에만
루트에 인후두 삐삐가 많이 나스 도트 a b 가 된다 라는 거 꼭
기억하셔야 됩니다
알겠죠 이거 하려고 지금 오늘 이 시간에
어 갖는 의미가 있습니다 이 시간에 갖게 될 의미입니다 이게 이렇게 됐지
그럼 또 볼까봐 아
두번째 우리가 볼 건 뭐냐면 루트 b 분의 또 루트 a 에 대해서
알아보자 2 거지
당연히 a 도 양수 고비도 양수인 경우에는
이런건 뭐가 된다라고 배웠냐 하면 루트 b 분의 에이다 이렇게 알고
있습니다 이번 중학교 때 배운 겁니다 자 그러면 우리는 바
붐 모아 분자가 음수 고 분모가 양수인 케이스를 한번 알아볼까요
그럼 보자 루트 b 분의 루트에 이라는 놈은 루트 b 분의 또 같이 쓰면
됩니다
루트에 - ai 가 되구요
요놈은 양수자 나 이제 - 얘기가 그러면 일본에 의해서 여러분 노트 b
분의 - a 의 아이가 됩니다
그런데 우리가 알고 있듯이가 루트 안으로 들어오면 뭐가 되니까 -
를 만드니까 마이너스의 - 가 돼서 이것은 b 분의 게임 요렇게 된거죠
즉 분자 만 0보다 작을 경우에는 루트 b 분의 루트 2는 그냥 루트 b
분 a 가 되는겁니다
이렇게 그럼 이번엔 따라 세 번째 a 가 양수 고비가 음수 인 경우를
한번 보자 일과 통해 는 루트 b 분 의 루트에 이잖아요
얘는 루트 - b i 분해 해 루츠 a 다 되고요
그 정 자 요런 양수 됐으니까 이제 일본에 의해서 여러분 노트 - b
분의 a 가 되는거고
아 2분의 1 이렇게 된겁니다
자 그럼 우리는 뭐 부모의 실수 알을 해주기 위해서
요 분자 부모의 요 놈의 켤레 복소수 인 - i
그다음 분자 에도 - 아이를 고파 게 되는 거죠
그점 그럼 이제 어떻게 되나 볼까 그러면 아이유와 - 아이가 곱해 지면은
- 아 이제 봄이니까 1 됩니다
그지 예 그러면 봐라 요놈은 결과적으로 남는 놈은 루트에 - b 분의 a
에 1분에 - 아이가 되는거고
자 - 요 - 는 그냥 앞으로 빼주고
아이를 누 츠 안으로 넣어 준다고 생각하면 부가 바뀌면서 요렇게 됩니다
자 그래서 또 여러분이 꼭 중요하게 기억해야 될 게 분 몸안 0보다 작을
경우에 루트 b 분의 루트에 있는 - no 5 피부 노트 피부 a
가 됐다는 겁니다
여기서 중요한 건 요 앞에 - 입니다 - 됐지
그럼 하라 우리가 한 가지 안 봤잖아
네번째 2 당 0보다 작은 경우 엘보 잘까 이렇게
그러면 루트 삐 분의 루트에 이라는 놈은
루트 - b i 분해 루트 - 이가 되는거고
자 ii 는 그냥 약불에 주면 되고요
이거 둘다 양수 니까 - b 분 의 - a 가 되는거고
- - 약 뿐 되면 이렇게 된다는 걸 볼 수가 있는 거죠 그래서 이
경우도 자연스럽게 그냥 루트 b 분의 에이다 이렇게 되는 겁니다 자 결국
여러분이 기억해야 될 거 뭐냐 하면 다 아 그저 대부분의 경우 루트에
이브의 노트 b 는 루트 b 분의 a 가 되는데 딱 한 가지 경우 즉
분자는 0보다 큰 데 분 보우 탄에 들어 이놈이 0보다 작을 때에는 루트
삐 분의 누트 a 가 - 앞에 달고 요렇게 된다는거
요거 꼭 기억하셔야 됩니다 개 이건 무장에 중요한 겁니다 무쟈게 중요한거
됐죠 그래서 자 오늘 오늘 배운걸 정리합니다
그럼 한 가지 경우 a 가 0보다 그가 짧고 b 가 0보다 작은 경우 만
루트 a 루트 b 는 앞에 뭐가 붙는다
마이너스 루트 a b 가 된다 라는거
그다음 a 가 0보다 크고 p 가 0보다 작은 요 한가지 경험한 루트 삐
분의 루트 a 가 마이너스 루트 b 분의 a 가 된다는 것 꼭 기억해
주시기 바래요
이렇게 자 그러면 이런 것들은 이제 어떻게 문제의 등장을 하냐면
예를 들면 본연 식입니다 그저 a - 2 루트 푸네
목 a+ 일에 루트가
많이 났을 노트 a - 2부 4
a+ 일이 되었다 이렇게 조건으로 주어 져요
그럼 이 얘기 뭐냐 아 a - 이는 음수 고 a+ 일은 다 잘 보면 물론
내가 우리가 양 수 인 경우만 다룰 수도 있지만
분자 다영이 되버리면 양쪽이 똑같아 지기 때문에
요건 요렇게 쓸 수도 있겠죠 그저 그래서 우리가 요런 조건이다
즉 개인은 - 일보다는 크거나 같고 이 보다는 작은 범위 있다
나는 u 조건을 요런식으로 줄 수가 있다라는 겁니다
이해가 대정 그저 네 그래서 요 것만 기억하시면 되요
물론 위의 걸 이용해서도 우리가 똑같은 경우를 볼 수가 있구요 됐죠
ok


댓글 0개
등록된 댓글이 없습니다.