수학중독 이차함수의 최대와 최소 > 중학교수학

 

이참 술 최대 최소 는 이차함수의 그래프 만 그릴 줄 알면 아주 쉽게
구해 낼 수 있는 각 드립니다
따라서 여러분들이 전혀 긴장 할 이유가 없죠 이미 우리는 이 참수 의
그래프를 그릴 수 있기 때문에
자 왜 그런가 한번 볼까요 이참 수에서 이창 의 개수가 양수인 경우에는
이런 식으로 아래로 뽈록이 이 참수 의 그래프를 얻을 수가 있구요
이창 의 개수가 음수 인 경우에는 이와 같이 위로 뽈록이 니 참수 의
그래프를 얻을 수가 있습니다
잠 아냐 실수 전체 구간에 대하여 이 함수의 최대 또는 최소값을 구하여라
라는 문제가 나왔다면
당연히 이 함수는 최소 까 밖에 존재하지 않구요
이 최소값은 소위 말하는 이 참수 폼을 썽 그저 포물선의 꼭지점의
존재한다.는 걸 우리가 알 수가 있습니다
가장 낮은 점이 되겟죠 그 다음 이 경우에 위로 폴록 이남수 에서는 최대
까만 역시 포물선의 꼭 직접 그 정 a 참수 그래프의 꼭지점의 서
존재한다. 갖게 된다 최대값을 요걸 우리가 알 수가 있습니다
자 그래서 우리가 아래로 뽈록이 남순은 최소값 위로 뽈록이 남순은 최대
깜 만 존재한다. 이렇게 알고 있는데
만약에 x 에 범위가 주어지고 그 범위 안에서 최대 최소값을 구하여라
나는 문제가 주어졌다면 어떻게 할거냐 라는 거야 자 그 경우를 우리가
한번 보도록 하죠
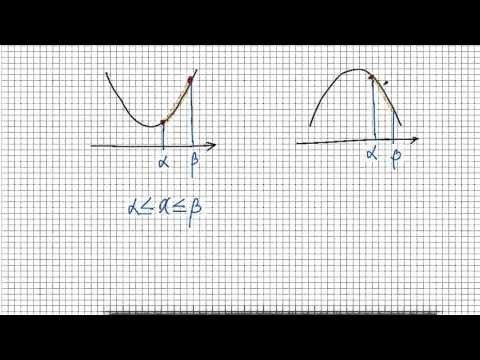
예를 들어 요기가 알파 고 요기가 벨 탑니다
그 정 x 의 범위를 우리가 알파 보다는 크거나 같고 베타 보다는 작거나
같다 로 한정하고
요 범위 내에서 2 이차함수의 최대 최소 값을 구하라 라고 했다면 어떻게
될 거야 자
너무 쉽죠 왜 우리가 봐야 될 구간은 바로 요기 알파 에서부터 베타 까지
따 요구 아닙니다 요구가
요 구간에서 우리는 가장 작은 값과 가장 큰 값을 찾으면 되는데 이건 뭐
그저 유치원생도 찾을 수 있죠
봐 가장 작은 값은 여전히 꼭지점의 있는 요 각시 되겠구요
가장 큰 값은 가장 높이 있는 요점 에서의 값이 최대 값이 된다 라는 걸
볼 수가 있습니다
그렇죠 너무나 쉽다 는 말이야
이 경우도 마찬가지입니다 자 예를 들어서
알파 고 베타를 요기가 알파 고 요기가 베타 라고 한번 해볼까요
역시 x 의 범위를 알파 보다 크거나 같고 베타 보다 작거나 같은
구간으로 1 정한 다음에 이 구간에서 에 최대 최소값을 구하여라
라고 문제가 나왔다면 우리는 그래프 중에 딱 요 부분만 보면 된 겁니다
알파 에서부터 베타 까지 그려진 구간
그리고 이 구간에서 가장 큰 값과 가장 작은 값을 찾아 내면 되는데
여전히 가장 큰 값은 꾹 직접 에서 받게 되고요
가장 작은 값은 이 구간에서 가장 낮은 점 요점을 찾아 내면 되는 겁니다
너무 쉽죠 그래서 알파에서 의 함수 값이 최소 값이 되는 것을 볼 수가
있는 거죠
그저 3 일단 그림으로 최대 최소 가 어디있는지 만 우리가 찾아보도록
합시다
자 그런데 예를 들어 그래프가 이렇게 그려진 상황에서
예 덩이가 x 의 범위가 꼭짓점을 포함하지 않는 범위로 주어졌다 즉
요기가 알파 고 요기가 베타 없다라고 생각을 해봅시다
x 는 알파 보다 크거나 같고 베타 보다 작거나 같은 범위 내에서 이
함수에 최대 최소값을 구하여라 라고 한다.면 당연히 우리는 역시 요구가
안에서만 예 최대 최소값을 구하면 되구요
최소값은 가장 작은 값이 알파에서 의 함수 값이 최소 값이고 최대값은
가장 큰 값인 베타에서 의 함수 값이 최대 값이 된다 라는 걸 알 수가
있습니다
이거는 위로 뽈록이 되더라도 예 저녁 달라지지 않겠죠 그 정
예를 들어 알파가 어디라고 할까 뭐 알파가 여기 라고 할까
요렇게 봅시다 요기가 알밥 뭐 요기가 베타 요렇게 됐다면 알파에서 베타
사이 까지만 우리가 보는 거니까
요 범위 내에서만 생각하면 되구요 당연히 최대값은 알파 에서의 함수
값이고 최소값은 배탈 의 함수 값이 됩니다
자 그래서 우리가 이차함수의 그래프 만 그릴 수 있다면
이차함수의 최대 최소 값을 찾아내는 건 전혀 문제될 게 없다 이렇게
말씀드릴 수가 있어요
자 그러면 예제를 보면서 우리 한번 그냥 연습을 해볼까요
y 는 x 의 제고 - ex
프라스 오라는 이러니 참 수가 있다고 해봅시다
e 참새 그래프를 먼저 그려 볼까요
그러면 이해는 다시 쓰면 어떻게 되요 x - 1의 최고 그 다음에 플라스
사회 꼬리 되겠죠
이렇게 우리가 완전 제곱 식으로 바꾼 이유는 다 알고 있을 겁니다
얼마만큼 평행이 독을 한도 민지 파악하기 위해서 크 해요
자 그래서 얘를 파악을 해 보면 얘는 y 는 x 제곱의 그래프를 x
축으로 얼마만큼 일만큼 y 축으로 얼마만큼 만큼 평행이 동안 그래프가
됩니다
맞죠 그러면 그래프를 이렇게 그리면 되겠네요
됐지 그래서 1 콤마 1 2 3 요기 쯤해서 요런식으로 요렇게
그래프가 생기는 걸 볼 수가 있습니다
요점이 바로 무슨 점이 되냐면 1 콤마 사인 점이 되는 거죠 그렇죠
자 그렇다면 바 아무런 조건 없이 2
e 창수 의 최대 깝 혹은 최소값을 구하여라
나는 문제가 나왔다면 그냥 e 참 수는 최소 깜 만 존재하고 최소
까 얼 말 갖는다
를 갖는다 라는 걸 우리가 볼 수가 있습니다
그렇죠 그런데 x 의 범위가 주어졌다고 한번 생각을 해보자 거야
예를 들어 x 는 0부터 이 사이에서 그저 e 까지 말고 3까지 한번
해볼까요
0부터 삶 사이에서 에 최대 최소값을 거야 라 라는 문제가 나왔다면
x 는 영은 여기쯤 2 여기쯤 니라 여기 줘 그럼 그 다음 맥스는
사람은 여기쯤 이렇게 있을 거다 이 거야 맞아
그럼 우리가 보려고 하는 구간은 바로 요 구간이 되겠죠 그럼 요
구간에서의 최대 최소값을 구하면 되는데
그림에서 금방 확인할 수가 있습니다
최소 깍 가장 낮은 정은 여전히 여기 꼭 직접 일하는 걸 우리가 알 수가
있구요
그다음 가장 높은 점 즉 최대값은 바로 이점이 된다 라는 걸 볼 수가
있는 거죠
그저 따라서 x 가 3일 때 의 함수 값이 요때 최대값이 되는 겁니다
그래서 이 경우는 바 우리가 이렇게 쓸 수가 있어요
최소값은 얼마 하고요
최대값은 얼마가 됩니까 x 에다가 사물 대의 평가 즉 여기다 우리 엑세스
인삼을 넣어 볼까요
그러면 이 이에 제곱 이니까 되죠 + 사니까 최대값은 파리 구나 라는
걸 우리가 볼 수가 있는 겁니다 됐죠
어려운거 하나도 없어요 오케이 그럼 예를 들어 우리가 이 부터 3사에서
보장
만약에 x 값을 2부터 삶 사이에서 보자 라고 했다면 이는 요기 쯤
있겠죠 요렇게 요기 이가 있을 테니까
아 우리가 보려고 하는 구간은 결국 여기서부터 여기까지 구나
그러면 파 여기서 에 최대값은 여정이 3회 서 의 함수 값이 맞구요
최소값은 2 에서의 한수 값이 최소 까치 된다는 걸 볼 수가 있죠
그럼 뭐 안 해 봐도 되겠죠 예 최소값은 이 해서 에 함수 값이 니까
요기 다이너 쓸 때 최소 까오 가 나온 것을 우리가 볼 수가 있습니다
그제 기왕 이렇게 된거 써봅시다 그래서 최소 오는 얼마가 되고 5가
되고요
최대 는 여전히 3회 서 의 함수 까 파리 되는 것을 우리가 확인할 수가
있습니다
됐죠 별거 없습니다 자 그 다음 바 하나 더해 봅시다 우리
와인은 예를 들어 뭐랄까요 - x 의 제곱 빼기 6x파스 cb 이정도
한번 해볼까요
얘도 우리가 완전 제고 거 로 바꿔주면 일단 요 부분을 요렇게 써야 될
거구요
마 점 그 다음에 - 에는 x 의 제곱 플라스 6 액스 플라스
9 요거 반에 제 곡 이라고 했습니다
요렇게 됩니다 맞죠 그다음 플러스 c 이렇게 되는거 4
그지 그럼 얘는 뭐가 되냐 하면 밥 - 의 x 플러스 3 의 새 고비
되구요
그 담요 마이너스의 - 가 묶이면서 펠라스 구가 되니까
요렇게 되는 것을 우리가 볼 수가 있습니다
됐죠 그럼 얘는 그래프를 대충만 그리면 됩니다
장애는 x 축으로 깍 결국에는 뭐예요
와인은 누구의 그래프를 - x 제곱의 그래프를 x 축으로 는 얼마만큼 -
3 만큼 y 축으로 는 얼마만큼 21 만큼 평행이 동안 놈이 됩니다
맞죠 따라서 그래프가 - 3 콤마 21에서 이런식으로 이렇게 그려 질
거라는 걸 우리가 알 수가 있구요
요점이 - 3 검마 20일이 된걸 볼 수가 있습니다
자 x 의 범위가 없는 상태에서 최대 또는 최소값을 구하여라
나는 문제가 나왔다면 당연히 에는 최대 까만 존재를 하고요
그때 최대값은 20 일이라는 걸 우리가 볼 수가 있는 거죠 그 정
만약에 x 의 범위를 - 5 부터 일까지 고 봤다 라고 한다.면 우리가
봐야 되는 그래프는 요오 요기 요 부분이 되겠구요
그때 최대값은 변함없이 꼭지점의 서의 함수 값 20일이 될거고 최소값을
당연히 뭐예요
이걸 얘가 더 장녀 애가 도장 냐는 물론 그림으로 판단할 수도 있겠지만
그저
요기 대칭 축에 x 좌표가 얼마냐 하면 - 미정
그러면 대칭 축에서 더 멀어지면 멀어질수록 더 작은 값을 간다 라는 걸
우리가 알 수가 있습니다
왜 대칭 축을 추구로 좌우가 대칭이 니까
그래서 이름이 대칭 축이 자나 그림 따라서 이래서야 함수 카피도 잡다
라는 걸 우리가 볼 수가 있는 거죠 그래서 이 경우에 최소값은 이래서야
함수가 즉 여기 다 잃는 얼마요
이것아 대면서 제 곱하면 16 - 16 a10 일이니까
요기가 함수 까오 를 갖게 되는 것을 볼 수가 있습니다
따라서 우리가 x 감 - 5 에서부터 1 이롭다 범위를 한정한 다음에
요구가 난 에서의 이 함수의 최대 최소값을 구하여라 라고 한다.면
최대값은 21 이구요 최소값은 얼마 5가 되는 것을 볼 수가 있습니다
됐죠 예 얼마든지 범위가 버 편 한다.고 하더라도 여러분들 충분히 최대
최소값을 구해낼 수 있을 거라고 믿습니다