수학중독 삼차방정식 근과 계수와의 관계 > 중학교수학

 

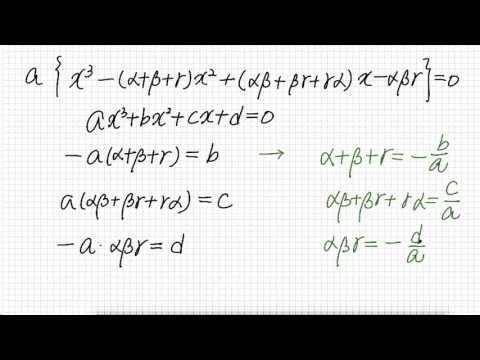
3차 방정식 근과 개수와 의 관계에 대해서 알아보겠습니다
우리가 이차방정식의 근과 계수의 관계 는 이미 배워서 알고 있죠
3차 방정식 근과 계수의 관계 도 같은 방법으로 우리가 살펴볼 수
있습니다
즉 무슨 일이냐 하면 ax 의 3 제고 플러스 px 의 제곱을 scx
플라스틱 올 영의 생애의 그들 알파 베타 감마 라고 했을 때 그저
이론들은 결국은 x - 알파 그다음 x - 베타 x - 감 말하는 인수를
갖게 될 테고 따라서 2 3차 식을 인수분해 하면 최고 찬 개수의 이를
맞춰주면서 요런 꼴이 될 거다 라는걸 우리가 알 수가 있죠 그렇죠
따라서 바라 얘네들을 전개하게 되면 어떻게 되냐면 요 아
에일은 그대로 두고 이거 우리 어디서 배웠어
그 곱셈 공식 에서 배워서 알고 있습니다
그저 근데 뭐 안되면 하나하나씩 전개를 해보세요
우리 그냥 배우는 입장이 니까야 하나씩 전개 해 볼까
그러면 앞에 거 2개를 먼저 전개를 하면 x 의 제곱 알파 프라스 베타의
x 플러스 알파 베타 가 되구요
여기에 다시 누가 5패 지능 거냐면 x - 감마 가 곱해 진 거기 때문에
자 곱하면 바 x 의 세제곱 - 감마 x 의 제곱 - 알파 플라스 베타
x 의 제곱 빼기 알파 플라스 베타의 뭐가 될 거야 아 이렇게 곱하면 +
가 되겠네요 감마 의 x 가 되구요
그 다음에 알파 베타 x - 알파 베타 감마
요렇게 됩니다 그렇죠 그럼 요거를 고대로 정리를 해주면 뭐가 되냐 하면
바 x 세제곱 있구요 x 제곱 있는 것들이요 놈과 요놈 이네요
즉 - 로 묶어 주면 요렇게 됩니다 플러스 감마 x 제곱 이 되구요
그 다음에 x 가 있는 놈들은 요놈 요놈 이니까 묶어주면 와 알파 베타
플러스 요거 또 전개하면 베타 감마 플러스 감마 알파 이렇게 되겠죠
요즘에 x 그다음 마지막으로 알파 베타 감마 이렇게 남게 됩니다
이거 전부다 에 누가 곱해 지는 꼴이야 a 가 곱해 지는 꼴이죠
맞죠 그래서 이거 이꼴 얼마가 된거 야 이거 이꼴 0이 된다 이렇게
보시면 됩니다
그러면 이해하고 이제 볼까요 예 하고 결국은
ax 의 3 제고 플러스 b x 의 제곱 플러스 cx 플라스틱 꼴 영희
똑같은 식이 되어야 되는 거잖아
따라서 팔아 3 제곱의 개수는 aa 끼리 똑같은거 알 수 있구요
그 다음에 제곱의 개수는 위에 놈은 요렇게 되네요
요렇게 되죠 그놈이 비랑 똑같아야 되고요
그 다음에 아 a 의 알파 베타 플러스 델타 감마 플러스 캄 마알 파의
경우는 뭐 해야 돼 씨가 되는걸 볼 수가 있습니다
또한 - 2 알파 베타 감마 라는 놈은 예 d 랑 똑같아야 된다는 걸 알
수가 있죠
따라서 우리가 얻을 수 있는건 자 여기에서
애인은 3차 방정식 이라고 했기 때문에 a 가 0일 인 없습니다
따라서 알파 프라스 벨 타파스 감 많은 - a 본의 비가 되구요
그 다음에 알파 베타 파 스펠 타 감마 플러스 감마 알파는 a 분의 씨가
됩니다
또한 알파 베타 감마 라는 놈은 다시 마이너스의 입은 의 d 가 되는 걸
볼 수가 있겠죠
요거 세계를 여러분들이 머리속에 외우고 계셔야 됩니다
됐죠 자 익어라 되게 재미 있습니다
우리 감에서 볼 수 있는게 뭐냐면
이차방정식 에서는 bx 플러스 씻고 용해서 얘 2 군이 알파 베타 라고
했을 때
자 큰 을 하나씩 더한 것은 마이너스의 입은 에삐 구요
그냥 그늘 2개씩 더하고 싶은데
2개 밖에 없기 때문에 아 2개씩 곱한 걸 더 하고 싶은데
흔히 2개 밖에 없기 때문에 알파 베타 1 만 나오게 되는겁니다
그래서 이걸 에이브 4시 라고 쓰는 거죠 그럼 하라
ax 의 3 제고 플러스 bx 의 제곱을 scx 플라스틱 꼴 영에 섹은
2 알파 베타 감마 라고 했을 때 작은 을 하나씩 더 하면 뭐가 되냐면
- 에이브 네비가 되고요
그늘 2개씩 곱해서 더하면 뭐가 될 거야 아 여러분 그냥 av 에 씨가
되는거구요
그늘 3개씩 곱해서 더하는 것
근데 근이 3개 밖에 없으니까 그냥 알파 베타 감마 1 떨렁 나오겠죠
이놈은 다시 마이너스의 이번에 d 가 되는 것을 볼 수 있다는 겁니다
이게 규칙성 있어요 그래서 그늘 하나씩 더한 것은 맨 앞에 거 분해
두번째 과의 - 그저 대충 요한 거니 부어 드립니다
요거 그저 그 다음에 그늘 2개씩 곱해서 더 한거는 맨 앞에 것뿐 에 세
번째 거 그 직 금이 것도 마찬가지야
그늘 하나씩 또한 것은 맨 앞에 것뿐 에 두번째 거에 - 그 정 그를
2개씩 곱해서 더한 것은 매
나 폐 것뿐 에 세 번째 건데 테마 스
그다음 그늘 3개씩 곱해서 더한 것은 먹으니 3개 밖에 없으니까 요거
하나 떨렁 나오겠죠
맨앞에 거부 네번째 거에 - 요케 된겁니다
규칙성을 알 수 있을까요 그 정 그럼 봐라
우리가 이 규칙대로 가자면 4차 방정식 은과 개수와 의 관계도 알아낼
수가 있어요 볼까
a x 의 제곱 플러스 bx 의 세제곱 씨 x 의 제곱 플러스 tx
플러스 이꼴 역 이해를 한번 보자
얘는 예 그늘 알파 베타 감마 델타 이렇게 4개 라고 해봅시다
작은 을 하나씩 더 한거 뭐가 될까요
예 여러분 당연히 - 이브 d 가 됩니다
맨앞에 거부 두번째꺼 해보라고 - 그지
그 다음 두 번째 글을 2개씩 또 하면 알파 베타 킬러스 알파 감마
플러스 알파 델타 플러스 베타 감마 플러스 베타 델타 플러스 감마 델타
요렇게 6개가 나올 거 아니에요
이름은 에이브 4시 이렇게 됩니다
맨앞에 그분의 세번째 거에 플러스
그 다음 글을 3개씩 곱하면 뭐가 될까요 알파 베타 감마 그 다음에 알파
베타 델타 그다음 알파 감마 델타 그다음 베타 감마 될 다면 뭐가 돼
다시 - 이번에 4번째 거
그래서 우리가 뭐 - 다 된다는거 보시면 되고요
그 다음 그들 네 개씩 곱해서 더 하는건데
그래봤자 요거 하나 떨렁 나오겠죠 여러분 다시 a 분 의 2가 되는 것을
알 수가 있다라는 겁니다
됐지 이러한 규칙성이 5차 6차 7차 백차 방정식이 되도 깨지지 않는다는
걸 알아 분들이 알고 계시면 되겠어요 됐죠 그래서 뭐 이것까지 여러분이
알고 있을 필요는 없습니다 우리가 4차 방정식 근과 계수의 관계 를 쓰는
일은 거의 없을 텐데 그냥 규칙성이 이렇다 라는 걸 보여주기 위해서 새
맴버 보여준 거에요
여러분이 기억해야 될 것은 바로 요러한 3차 방정식 근과 갯수 와의
관계에 그다음 이차방정식 근과 갯수 와의 관계 까지만 여러분 머리속에
갖고 계시면 될 것 같습니다
개쩜 어려운 거 없어요 자 그럼 바
우리가 이차방정식 에서도 이거 했지만 그래서 이제 우리는 3차 방정식 의
작성
이걸 한번 해보도록 하죠
3차 방정식의 작성
이름은 뭐 로부터 근과 개수와 의 관계로 부터 충분히 알 수가 있습니다
무슨 얘기냐 알파 베타 감마 를 섹은 으로 하는
3차 방정식 은 뭘까
3차 방정식을 구하세요 이런 문제가 나왔다고 칩시다
구하라 그저 솔로로 데뷔 했죠
자 그럼 바라 알파 베타 감마 를 세금으로 하는 3차 방정식을 구하라
라는 문제가 나왔다면
당연히 그 3차 방정식 은 x - 알파 그다음 x - 페타 그 다음에 x
- 캄 마이 꼴 영의 형태가 될 겁니다 자 물론 요놈은 3차 항 의
개수가 1일 때
3차 항 의 개수는 일이다
요렇게 주어졌을 때 얘기고 요 만약 이 5월 일반적으로 삼창 의 개수는
뭐 이었다 그럼요 앞이다 이만 곱해 주면 되니까 삼창 의 개수가 k 였다
라고 한다.면 요하게 케이먼 곱해 주면 되는 겁니다
그래서 이렇게 3차 방정식을 만들수가 있는데
근과 계수의 관계 를 이용하면 요걸 전개한 형태의 3차 방정식 또 만들수
있다는거 지 자 무슨 얘기냐 하면 바
알파플러스 베타 프라스 감마 가 뭐 예를 들어 보라 주 의 라고 할까요
그다음 알파벳 아 플라스 베타 감마 프라스 감마 알파가 라주 삐 구요
마지막으로 알파 베타 감마 가 라주 쓰였다고 한다.면 이 조건을 만족시키는
3차 방정식 은 당연히 앞쪽 인 케이가 곱해 줘야 되겠구요 x 의 세제곱
- a x 의 제곱 캘 sb x
그다음 - c2 꼴 0이 되는 것을 알 수 있다라는 겁니다
그 즉 이건 삼창 의 개수가 k 다라고 주어 졌을때 얘기입니다
따라서 우리는 스리 에 그늘 섹은 이 주어졌을 때 의 3차 방정식을 뭐
요런 식으로 표현하는 것도 가능하지만 요렇게 표현하는 것도 가능하지만
근과 계수 와의 관계를 이용해서 요런 식으로 표현하는 것을 할 수 있어야
됩니다
개쩜 예 이것만 되면 우리는 뭐 근과 계수의 관계 에서 나올 수 있는
문제는 다 풀 수 있다 이렇게 보시면 되요