수학중독 | 고차방정식 켤레근
본문
※ 영상을 선명하게 보기 안내
- 유튜브 영상에서 오른쪽하단에 톱니바퀴를 클릭합니다.
- 팝업목록에서 "품질" 선택하세요.
- 원하는 해상도를 선택해주세요.
※ 모바일에서 Wifi가 아니라면 데이타가 소진될 수 있으니 주의바랍니다.
수학중독님의 중학교수학강의 청각장애인을 위한 자막
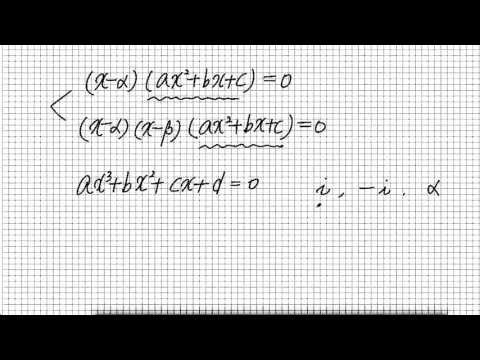
우리 이차 방정식을 배우면서 요 이런 내용을 공부한 적이 있습니다
예를 들어 a x 의 제곱 플러스 bx 8 sc2 꼴 영이 적 요 놈의
그게 수 들 즉 a b c 가 그저 a b c 가 모두 유리수 일대
그저 즉 유리 계수 일대 만약에 p 플러스 q 로 2m 2 1 그리면
예 당연히 어서 pq 는 유리수 구요
그 다음에 누트 m 은 뭐가 되 거야 무리수가 됩니다
얘는 왜 이렇게 맨날 이렇게 공간을 잘 못 찾을까 요렇게 쓸까요 4
루트 m 은 물이 숙
요런 상황에서 나머지 1건은 볼 것도 없이 뭐가 된다 그랬어
1 그리면 p - q 루 2m 도 큰 이다
요런 얘기를 했었죠 그저 그 다음에 이 이차방정식 에서 예를 좀 강조
표시를 해 볼까요 요 이차방정식 에서 a b c 가 모두 무슨 그리면
아 에 무슨 근니라 a b c 가 모두 실수 일대 그저 에 피
프라스 q 부트 보 아 q2 가 아니라
qi 라고 합시다 qi 저그 줘 q 아이가 한 그리면
네 당연히 pq 를 실수 입니다 그저 여기 갔을까요
pq 는 실수
p - q 아이도 아 그 이다
요런 내용을 우리가 배워서 알고 있습니다
여기 소위 말하는 이차방정식 에서 켤레 근 정 이었죠
그저 근데 이놈이 3차 이상의 고차 방정식 에 대해서도 성립합니다
즉 무슨 얘기냐 하면 우리가 고등학교 교육과정에서 배우는 3차 방정식
4차 방정식
뭐 혹은 더 나아가 5차 6차 가 나올 가능성은 거의 없지만 가뭄에 콩
나듯이 나온다고 하더라도 결국 걔네들은 인수 분해 를 통해서 우리가 많죠
그늘 구해낼 수 있는 형태라고 얘기를 했죠 따라서 바 3차 방정식 같은
경우에는 x - 알파 라는 놈을 끄집어내고 a x 의 제곱 플러스 bs
프라스 ce 꼴 영예 꼴로 바꾸어서 그늘 9 하구요
4차 밤 정식 의 경우에는 1차에 인수 x - 알파 x - 베타를
끄집어내 이후에 나머지 2차 식에서 2차 식 의 풀이를 통해서 모래 음
우리가 그늘 찾아낸다 라고 말을 했었습니다
이거는 뭐 늘 그런건 아니지만 고등학교 교육과정에서 는 그렇게 나온다 고
했죠
그랬을 때 만약에 켤레 근이 나오게 된다면 여기에서 나오게 될 거다 라는
얘기 아 여기에서 그지
만약에 알파 베타 나는 놈들이 그냥 정수 였으면 실수 인정 수 였으면
따라서 그냥 우리는 어떻게 생각할 수 있냐면
i 2차 식에서 만약에 허근 이 나오게 되면 당연히 켤레 복소수 인두 허
군이 나올 거구요
2 2차 식에서 2차 박경식 에서 abc 가 유리수 였을때 피파 쓰 q
루트에 미라는 물이 쑤실 근이나 왔다면 당연히 p - q 템도 크니 될
거다 라는 것 정도 여러분들이 알고 계시면 된다는 거예요
사실 이걸 또 정확하게 우리가 지퍼 내기 위해서는 고등학교 수준을
벗어나는 내용이 필요하긴 합니다 그래서 그냥 여러분들 지금 선생님이 말한
것처럼 아 고등학교 과정에서는 그냥 이렇게 되는구나 라고 이해하시면 되요
그래서 예를 들어 봐 못 3차 방정식 ax 의 3 제고 플러스 bx 의
제고 플러스 c ex 플러스 튀는 이꼴 용인데 abcd 가 모두 실수야
그런데 한 근이레 그럼 물론 아이를 여기다 대입해서 npc 길을
구해야 되겠지만 그냥 이런 경우엔 나머지 1대는 - 알겠구나
그러면 두 개의 근을 9 했으니까 나머지 그날 파만 구애 내면 되겠구나
뭐 이렇게 접근을 하면 된다는 거지
그래서 그날 가 주어지면 나머지 1근 그 지면 앞에다 마이클 쳤어요
그 나라 가 주어지면 나머지 한건도 쉽게 구해 낼 수 있다라는 측면에서
여러분들은 켤레 근의 정리를 꼭 알고 있어야 되는 겁니다 그렇죠
자 그 다음에 이 다한 방정식의 또 특징 이 있어요
예를 들면 바 우리가 fx 라는 이놈을 뭐 a n x n 쓰 우 플러스
am - 1 x 의 n - 1승 뭐 이런식으로 해서
a 원의 x 플러스 a0 로 끝나는 다음 시기라고 한번 해봅시다
얘네들은 그냥 n 차 시기 되는건데
그저 내림차순으로 정렬한 겁니다 그리고 계수 들 우리가 뭐 abcd 를
다 쓸 수가 없으니까 an an - 1a 1a 제로 이렇게 표현한 것
뿐입니다
자 그럼 박 방정식 fx 꼴 영의 큰 있을 거 아냐
익은 들을 우리가 n 차 방정식 이니까 n 개의 근이 있겠죠
그래서 이 각각의 그들을 그냥 k1 k2 뎅 에서 k 애니 다 이렇게
얘기를 해보자 얘가 또 얘들이 실 그 니들 허브 니도 관계없이 그 얘기
뭐냐면 결국 f 에 케이의 i 를 대입하면 입 꼴 0이 된다 라는
뜻이에요 단 아이는 1 부터 어디까지 겠어
엥 까지 의 값을 가질 수 있게 되겠지 요기까지 상황이 하십니까
그냥 냉차 방정식의 n 차 시기 꼴 용의 n 차 방정식 의 그늘 k1
k2 ok 애니 라고 한다.면 당연히 요기 x 대신에 k 아이들을 넣었을
때 0 된다 라는 걸 볼 수가 있는 거죠 자 그럼 아 이런 상황에서 예를
들어 가
방정식의 약간의 변형을 준단 말이야
예를 들면
방정식 x - c2 꼴 영의 그는 뭘까요 라고 물어본다면
우리는 항상 기억해야 될 게 바로 요 거란 거지 아 우리가 알고 있는 건
뭐 구나
f 에다가 ki 를 넣었을때 0 되는 걸 알고 있으니까
이때의 근 들은 어떻게 쓸 수 있냐면 잘바 x 는 ki 플러스 쓰이게 꾸
나란 걸 볼 수가 있단 말이야 왜
x 의심의 ki 플러스 c 를 누르면 플러쉬 와 - 2 가 없어지면서
결국 fl ki 만 남게 되는데 그 도미 꼴 0 되는 건 이미 우리가
알고 있기 때문이다 이렇게 보시면 되요
따라서 이 해에 의 그는 바로 x 는 k-ifrs 씨들이 되는겁니다
당연히 아이는 1 2 해서 어디까지 n 까지 가 되겠죠
태초 이런 식의 그지 약간의 변형을 줬을 때 그도 여러분들이 구애 내셔야
된다는 뜻이 됩니다
그리고 한번 여러분 생각해 봐 만약에 sex 있고 0
자 요런 방정식의 그런 뭘까 라고 물어본다면 이외에 방정식의 그는 잘
보세요 x 는 뭐가 되겠어
당연히 쓰 2분의 ki 가 되 겠지
그지 뭐 아이는 여전히 1부터 n 까지 의 자연수 구요
이 경우에 쓰이는 0이 되면 안 될 겁니다
다 해주시는 영니게 찍으러 매터 용 인건 까이 건당 정식이 될 수
없습니다
됐죠 ok 그나마
fx 분해 일에 그는 보겠어 예 이꼴 영의 그는 당연히 x 가 바로 ki
분 의 일이 되는 겁니다
단 여기서도 ki 가 0닌 케이스를 보면 되겠죠
물론 영니니까 요런 식의 방정식이 나왔겠지만 그지
그래서 이런 식으로 방정식 뜰이 약간의 변형이 일어났을 때 의 근 들도
원래 변형이 일어나지 않 켜 일어나기 전체 fx 있고 영에 흔 들을
이용해서 구해낼 수 있는 능력이 여러분들한테 있어야 된다 라는 것
끄적 뭐 많이 나오는 건 아니지만 가끔 나와서 여러분을 괴롭힐 수 있기
때문에 그냥 뽀나스 차원에서 한번 얘기를 해줬습니다 됐죠


댓글 0개
등록된 댓글이 없습니다.