수학중독 내분점과 외분점 > 중학교수학

 

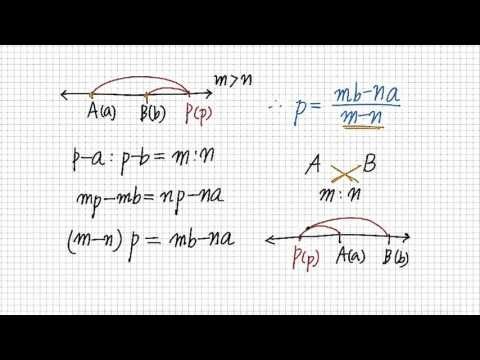
4군 점 과외 군 점에 대해서 알아봅시다 2
내분 점 과외 군 점 공식은 고등학교 수학 교육과정 내내 여러분들이
유용하게 써먹을 수 있는 공식입니다
따라서 한번에 완벽하게 이해하고 그 다음 공식 또한 완벽하게 외워 두셔야
됩니다 알겠죠
자 먼저 4분 전부터 봅시다 4분 점은 어 이게 안내 짜잔 아 그래서
안쪽에서 나누는 점이 다 이렇게 보시면 됩니다
예를 들면 이거 바울이 가 수직선을 그려 생각해 볼까요 먼저 수직선
위에서
여기에 이라는 점이 있어 예 좌표는 그냥 에 이구요 그다음 b 라는 점이
있는데 요소 아편은 비하 수직선 위 니까
그런데 우리가 이 ab 를 m 덴 으로 내부 나는 점을 한번 생각해 보자
라는 거지 그 지 금 이 m 덴 으로 내부 나는 점을 우리가 p 라고
하고 예 좌표를 우리가 소문자 p 로 나타낸다 고 한다.면
애가 엔드 애니 된다는 얘기가 뭐야
결국은 요 길이 대 욕 길이가 m 대해 애니 된단 얘기고
수직선 위에서 의 길이는 큰 쪽에서 작은 쪽을 빼주면 되는거니까
p - a 2대 b - 피가 m n 이렇게 되는 거야 그지
아따 서예를 우리가 이제 구하고 싶은 건 피자 나요
그죠 그럼 볼까 mb 어서 많이 듣던 그저 이니셜이 네요
mp 는 그 다음에 np - na 요렇게 우리가 쓸 수가 있다는 거지
그지 그럼 우리가 구하고 싶은 건 피자나 p
따라서 파 n+ 앤 의 피가 되는 거야 이거 이쪽으로 넘겨서 묶어 버린
겁니다 이거 넘어오면 뭐가 되냐 하면 어
mb 플러스 na 이렇게 됩니다
그제 따라서 우리가 얻을 수 있는 이 4분 점이라는 것은
피라는 높 은 어떻게 얻을 수 있어 m+ n 분해에 그저 mb 플러스
na 다 이렇게 얻을 수가 있는 겁니다
배 점 여러분 요 공식을 반드시 알고 있어야 돼요
그제 그래서 이걸 어떻게 했느냐 바
이거는 그냥 이렇게 하면 됩니다 a 가 있고 비가 있어요
그래서 여름이 순서가 중요합니다
ab 를 해낸 으로 내부 나는 것과 ba 를 m 댄 으로 내부 나는 것은
완전히 다릅니다 그지
그래서 이렇게 엔데 애니 라고 써주시면 예 보는 바와 같이 내분 점 은
래쪽에 누가 와야돼 n+ 애니 오면 되구요
그 다음에 이렇게 x 자 크로스 로고 팝니다
그래서 md plan a 이렇게 우리가 곱한다. 라고 생각하시면 되요 됐죠
예 그랬더니 어떤 학생이 선생님 이 na 부터 쓰고 mb 나중에 쓰면
안되나요
당연히 될지 그 중에 그렇지만 외울 때는 mbps na 로 외워두세요
자 왜 그런지는 조금있다가 우리가 외부는 점 을 공부할 때 고대로 이유를
알게 될 겁니다 ok 됐죠 자 그럼 보장 아 우리가 왜 문 점 에 대한
얘기를 또 한번 해보자 거야 그럼 왜 부쩍 으
외운 점은 어떻게 되느냐 밑으로 쭉 내려 갈까요
외국인 점은 또 수직선 한번 끓여 봅시다 수직선을 이렇게 그린 상태에서
그제 에 예를 들어 여기가 a 아 당연히 좌표는 이렇게 되구요 여기가
삐아 당연히 좌표는 이렇게 되는데 여기 어디 쯤에 누가 있냐면 피가 있는
거지
p 라는 점이 있는데 이제는 바 이 길이 돼 요 길이가 엔데 애니 되는
거야
이런걸 우리가 ab 에 안쪽에 생기는 분 점 니라 ap 에 바깥쪽에
생기는 분점 이기 때문에 그지
이걸 외에 분점 이다 라고 얘기를 하는 겁니다 됐죠
근데 이것도 쉬워요 예를 들어 애가 m 대해 애니 되면 어떻게 되냐면 파
p - a 대 p - p 가 m 데엔 이러면 된거 아니냐 이 거지
흠 똑같아 안에 꺽기 리고 팡 거 np - mb 는 그저 np 백의의 네
이렇게 됩니다
자 넘겨서 정리해볼까요 m - n 에 피로 묶어주시면 결과적으로는 뭐가
될 거야 넘어가면 mb - na 이렇게 됩니다
자 따라서 따라서 우리가 외부 문 점 피해 좌표는 m - n 분해에 앤비
- na 가 된다 라는 겁니다 됐죠
금 이것도 퇴원 야 차 바 a 하고 b 가 m 데에 너로 왜 문 않은 점
a b 를 mdm 으로 외부 나는 점은 자 외 분점이 면 2개를 뺍니다
n 에서 n 을 빼주고 역시 크로스 입니다
그저 크로스 인데 이 와 mb - na 아 즉 예부터 써주고 - 예 라는
얘기지
그 짐 그러나 아까 선생님이 4군 점 구할 때도 na 플러스 m 2 로우
지 말고 mb 플러스 na 로 왜 오라고 했잖아
맞아 예 그래 왜 그래
크게 외 군 점 에서 누구 에서 누굴 빼는 지 헷갈린 이까 그냥 내
분점도 mb 부터 시작하고
왜군 점도 mb 부터 시작하자 말이야 그 의 mb 이거 어디서 많이
들어본 이 절절한 외의 싶다 이 거야 맞아
그래서 우리가 mb 플러스 na 가 내분 점이고 mb - na 가 왜
분점이 다 이렇게 외워 2시면 에 틀릴 일이 없다 이가 됐죠 자 그럼 바
우리가 내분 점 외부는 점 공식을 다 왜요 그랬습니다
여러분들 외 분 점에서는 좀 알아야 될게 있어요 몰아야 되냐면 과 암
만약에 a 가 여기고 비가역 인데
p 라는 놈이 비의 바깥쪽에 생기는 거지
그럴 경우 그저 이런 경우는
m2m 보다 어떤 경우야 그의 그림에서 보시는 경우는 m2n 보다 큰
경우 입니다
따라서 이 길이가 이 bp 의 길이보다 더 크죠
자 그러면 만약에 m2 엠버가 작은 경우는 어떻게 되느냐
자 이렇게 된 거야 우리가 수직선 1 그리면 예를 들어 여기가 2이고
여기가 삥 거지 그 즉 그러면 피가 오른쪽에 생기냐 하면 이쪽이 생긴다
이렇게
그저 뭘 실력으로 가게 될 거야
피가 이렇게 생긴 다가 왜 그러면 방 ap 와 bp 요 길이 중에요 개
m 대해 애니 되어야 되는 거니까 아이 경우는 누가 더 크구나 m2n
보다 더 크거나 이렇게 된겁니다
따라서 그 ab 를 외부 난거 와 pa 를 외부 나는 것도 순서가
중요하고요
그다음 애미 더 클 때에는 비에 바깥쪽에 생기고 그 다음에 애니 더 작을
때에는 a 에 바깥쪽에 피가 생긴다는 거 이거를 기억하시면 되겠습니다
됐죠 그래서 어떤 경우든지 공식은 이거 아니까 여러분이 외워야 될 것은
요 공식만 정확히 알고 계시면 됩니다
됐으니까 자 그럼 바하 우리가 수직선 위에서 의 내분 점
외부인 점 을 알아봤다 말이야 그러면 평면에서 에 내분 점 한번 알아보자
평면에서 의 4분 점은 어떻게 되느냐 라는 건데 이거
아주 쉽다 이 거지 자 예를 들면 우리가 그냥 요렇게 요렇게 그려 볼까요
요렇게 있다고 치자 가 여기가 a 야 여기는 x1 y1 이야
그다음 여기가 삐아 여기가 x2 y2 라고 합시다
이렇게 좌표가 주어져 있을 때 ap 를 m 댄 으로 대부 나는 점 을
구하여라 이런 문제가 나왔다고 치자 이 거야 그 정 그러면 이게 어떤
식으로 되냐면 잘 반함
우리가 m 덴 으로 내부 나는 점을 요 점이라고 한다.면 여기가 요 길이
대요 길이가 m 대해 아닐 거 아니야
그치 요즘 크게 그려 볼까 너무 조그맣게 끌었다
요 지워버리고 좀 크게 그려 보자
영이를 쭉 크게 쭉 크게 그려서 여기가 x2 i2 라고 해보자 이 거지
그지 그리고 요기 어디쯤 2 요 길이 대해 요기가 m 대해 애니 되는 p
라는 점이 있다 라고 합시다
그래서 p 점 의 좌표를 우리가 뭐라 그럴까 요기를 그냥 x3 y3 라고
할까요
그저 이렇게 빨리 났다 이렇게 한번 바꿔보자 그래서 여기가 x3 컴 마와
이슬이 다 이렇게 한번 써보자 이 거지
그지 그럼 방 얘를 어떻게 고함 되냐면
요렇게 우리가 직각 삼각형을 그립니다 이렇게
그리고요 내분 점 피해서 예
요렇게요 논과 평행하게 그다음 요기서 또 요런 식으로 아래 요놈 과
평행하게 연결을 해주면 어떤 일이 벌어진다면 잘가
요기 리드 요 길이가 임대인이 니까 당연히 요고 때 요것도 m 대니
됩니다
게다가 그저 욕 일이 되 요 길이도 md 에 애니 되는 거야 맞아
그럼 보자 여기서 x 좌표 들만 본다면
요 점의 x 좌표는 x1 이지
그다음 요즘에 추자 편 얼마나 되는가요 점의 좌표는 x 투고 요점 x
좌표는 x3 가 된다 이거
그 다음에 y 좌표 만 본다면 요즘에 y 좌표는 y1 이지 요즘에 y
좌표는 y3 고 요 점의 y 좌표는 y2 가 되는 거야
그러면 봐 결국 잎이 점 에서 우리는 x3 y3 만 구하면 되는 거잖아
그런데 몰아 요것도 요구가 md 애니라 그랬어요 게 길이가 에 맨 이란
얘기가 아니라 길이의 비가 임대인이 란 얘기입니다
그러면 이 놈과 이 전체가 닮은 꼴이기 때문에 옛 5m 대인 된 거잖아
그렇게 따지면 얘도 m 대인이 되니까
결과적으로 x3 라는 이놈은 x 원과 x2 를 m 댄 으로 내분 한다.
라고 보시면 됩니다
자 따라서 x3 는 뭐가 되냐 하면 m+ n 분의 그지 크로스 라고 했다
mx2 플러스 nx 원이 되는거고
맞아요 그 다음에 y 좌표 끼리만 본다면 와 있으리라는 이 좌표는 왕이
원과 y2 를 m 대해 으로 매부 나는 좌표 기 때문에 y3 는 m+ 앤
분의 크로스 입니다
n y2 이렇게 되겠네 그제 플라스 ny1 요렇게 우리가 구할 수가
있다는 거지
따라서 따라서 결과적으로 우리가 얻는 잎이 점의 좌표 라는 것은 npr
sn 분의 x 좌표 써 주면 되잖아 mx2 플러스 nx 원이 되고요
커마 m+ n 분의 뭐가 될 거야
my 투 플러스 nyeon 이렇게 우리가 쓸 수가 있는 거야
x 좌표 따로 내분 점 구해 주시고
y 좌표 따로 4분 점 구 해주시면 된다는 얘기가 됩니다
간단하죠 x 따로 y 따로 이렇게 하면 될 거야 그러면 어때
왜군 점도 똑같았다 왜 분점도 그제 평면에서 에 왜 분점 한번 볼까요
평면에서 의외 분점도 우리가 똑같이 구할 수가 있어 예를 들면 얘도 그림
그려 보자 이렇게 그제
만약에 이거 요놈이 a 아 요 점의 좌표가 x1 y1 이고 요놈이 삐아
여름에 좌표는 x 탓 x2 y2 가 되는 건데 우리가 m 덴 4군 점 을
구한다. 그랬을 때 애니 더 큰 경우 보자 me 더 크다면 에 b 의
바깥쪽 여기에서 p 라는 점이 생길 거고 x3 y3 이렇게 될거 아냐
그러면 이 길이 돼 요 길이감에 땜에 시라고 m 데엔 용해된다 해봐라
마장 검기에 도 똑같아 이 똑같다 어떻게 여기서 이렇게 그려 버려
직각 삼각형을 그 다음에 연장을 이렇게 그려 버리면 똑같이 그럼 팔아
여기서 요 점의 x 좌표는 요즘에 액션 표는 x2 고요 점액 백수 좌표는
x 리 잖 아 근데 우리가 뭘 하느냐
아 요것도 요 길이 대요 길이감에 때 메시아 n 데엔 여기 된 거야 그지
그 다음에 여기에도 이렇게 연결을 해야지
그렇게 본다면 결국 파 요기에 좌표는 x y 투가 되나요
그저 여기는 x 가 아니라 y 투가 되고 요즘에 y 좌표는 y 원이고
요즘에 y 저편 y3 니까 결국은 또 욕 일이 돼 어디가
요 길이가 m 데 nd 받아 이 거지 그제 예
결국은 얘도 x 좌표 끼리 따로 y 좌표 끼리 따로 내분 짜가 외 분점을
9 해주시면 되는 겁니다
결국 한번에 갑시다 얘는 p2 점 의 좌표는 그지
아 my 너스 n 분해에 x2 - x1 커마 m - n 분해에 m y2
- ny1 요렇게 우리가 쓸 수가 있다라는 겁니다 됐죠
그래서 봐 결국은 수직선 위에서 의 내분 점
외부 분점 만 여러분이 제대로 알고 있다면 공식을 그집 평면에서 에
외부인 점 내분 점은 그냥 x 좌표 들끼리 의 외부 문 점 내분 정 커마
y 좌표 들끼리 의 외 분점 4분 점으로부터 우리가 구해낼 수 있다라는
거야
그새 이 삼각형 들이 전부 다 닮은 꼴이기 때문에 길이의 비가 계속
유지된다 이 거지 x 길이 따로 보던 y 길이 따로 붙어 ok
그래서 여러분이 고 것만 하시면 에 2 그 수익성 위에서 의 내부적
외부적 공식 평면에서 앱 운정 왜 분점도 우리가 쉽게 구해 낼 수가 있게
되는 겁니다
알겠죠