수학중독 직선의 방정식 > 중학교수학

 

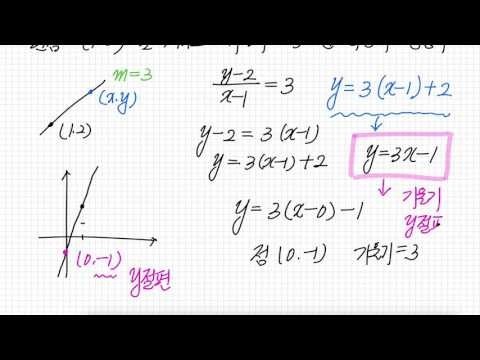
지난 시간에 우리 직선의 결정 조건에 대해서 알아봐 쬲
예 직선의 결정 조건은 1점과 기울기 라고 말씀드렸습니다
자 그러면 이제 한전과 기울기 라는 정보를 가지고 우리가
직선의 방정식을 표현하는 방법에 대해서 알아보도록 하죠 자 예를 들면
이렇게 직선이 있구요
이 직선 위의 한 점 x1 y1 이 있다라고 합시다
즉 이 직선은 x1 y1 을 지나는 직선이 다 이렇게 생각 하시구요
그 다음에 이 직선의 기울기가 얼마다 이 기울기가 편의상 그냥 애미다
라고 한 번 표현을 해 봅시다
즉 우리가 이제 해야 될 일은 기울기가 m 이고 한 점 x1 y1 을
지나는 직선의 방정식을 구해야 되는 겁니다 자 그런데 파악 직성이 라는
것은 결국 점들이 모여서 되는거구요
이 점들이 어떤 규칙성을 가지고 모여 있는 지를 우리가 수학적으로
표현하면 되는건데
그러기 위해선 우리가 이 직선 위에 이미 의 점을 하나를 더 잡아서 예를
x 콤마 와 이라고 2 겁니다
즉 직선 위의 임의의 점을 잡았다는 얘기는 ex 콤마 와인은 어떤 고정된
한 점니라 직선 위에 있는 점들을 일반적으로 나타내 주는 점이 다
이렇게 보시면 되요
무슨 얘긴지 모르겠죠 즉 직선 위에 있는 점들은 x 콤마 와 일하는
애들이 보여서 직선을 만들고 있다라고 생각하시면 되구요
우리가 구하는 이 직선의 방정식 이라는 것은 결국 몰고 하는 거냐면 바로
xy 점이 져 이점에 액수 좌표와 y 에 관계 식이다 이렇게 보시면
됩니다
이게 바로 직선의 방정식 예요
무슨 얘긴지 알겠습니까 자 그러면 일단 직선의 방정식을 9 해놓구 다시
한 번 얘기를 하면 아 고개가 끄덕여 질 있게 돼 끄덕여 지게 될 거에요
자 보도록 할까요
발아 기울기가 m 이라 그랬잖아
그런데 이 직선 이라는 것은 어느 이 직선 위의 어느 2점을 잡아서 기
우리를 9 하더라도 항상 일정하게 나와야 됩니다
그렇겠지 이 직선이 갖는 고유한 특징 중에 하나가 기울기 이기 때문에
어떠한 부 점을 잡아서 기울기를 구해도 똑같은 값이 나와야 된다는 거야
뭐 예를 들면 2x 콤마 y 라는 점과 x1 y1 을 이용해서 기울기를
9 1
아니면 뭐 요 점화 요즘 두개를 이용해서 기울기를 9 1
똑같은 값이 나와야 되겠죠 왜냐하면 이 직선의 기울어진 정도는 똑같기
때문에 그지
따라서 우리는 이 기울기 m 이라는 놈을 어떻게 표현할수가 있냐면
이렇게 x 102 x 원 부 내외 와인 - y 원이다
요렇게 표현할 수가 있게 되는 겁니다 자 그 다음에 우리는 그냥 쉽게
양변에 x 102 x 원 을 곱해 주는 겁니다
그럼 어떻게 되냐면 ml x - x 원은 y - y1
이렇게 되는거구요 정리해주면 와인은 애매 x 102 x 원 플라스 yu
이런 식으로 표현이 가능하게 되는 겁니다 자 그럼 바
아까 뭐라고 했냐면 결국 이 직선의 방정식 이라는게 x 와 y 의
관계식을 구하는 거다 라고 얘기를 했는데
보시면 딱 나오죠 x 와 y 가 이러한 관계식을 가지고 있다는게 딱
편익의 됐단 말이야
맞아 그 즉 그 다음에 발아 1 점이라는 것은 지금 어디에 들어가 있냐면
요 우리가 1정을 x1 y1 을 한 점이 라고 했다면 바로 여기에 x1
y1 이 들어가 있구요
그다음 기울기에 대한 넘은 여기에 딱 들어가 있게 될 것이
그래 그래서 요 5
직선의 방정식 즉 ex 콤마 와 의 관계 시계 특징을 조금 살펴 보면요
잘바 얘네들은 x y 에 대한 x 또는 y 에 대한 1차 시계 꼴로
표현이 되구요
그 다음에 x 의 개수가
x 의 개수가 언제 y 있는 해서 x 에 대한 식으로 y 를 표현했을 때
x 의 개수가 바로 기울기가 된다는 걸 아시면 되고요
그 다음에 x - x1 그다음 플러스 y 원의 형태로 원래는 x2 -
x1 y - y 원의 형태지만 우리가 넘겨서 정리 했기 때문에 요러한
형태로 1점이 반영이 된다는 것을 기억하시면 되겠습니다
요게 바로 우리가 구하고자 하는 직선의 방정식의 되요 이게 잘 모르겠죠
잘 모르겠으니까 우리가 예제를 한번 보면서 생각해 보도록 합시다
예를 들면 1점
뭐 1 콤마 e 를 지나고
기울기가
3인 직선의 방정식은 뭐가 되겠느냐 라는 겁니다 그렇죠
그러면 우리가 해야 될 건 똑같아요
다 이렇게 되는 거지 여기가 잃고 마이가 되는거고
이 직선 위의 임의의 점을 x 콤마 y 로 두는 겁니다
그리고 우리가 아는 이 직선의 기울기는 3 이다 라는 걸 알고 있는 거죠
자 배운 대로 가자면
x 102 1 그 다음에 y - 2 이라는 요 노 즉 기울기가 삶 이란
걸 알고 있기 때문에 우리는 어떻게 쓸 수가 있냐 면화 2 - 이라는
놈은 3 의 x - 길이 되고요
와인은 3 의 x - 1+2
다시 정리하면 와인은 3 x - 1
요러한 우리가 직선의 방정식을 얻어낼 수 있게 되는 겁니다
이해가 되십니까 요게 바로 우리가 최종적으로 구하고자 하는 직선의
방정식의 되요
자 보시면 그 정 x 와 y 에 대한 1차 시킨게 활 확인이 되구요
그 다음에 x 앞에 개수가 바로 기울기와 똑같다는 걸 볼 수가 있습니다
그리고 물론 한 점을 나타내는 정보를 우리가 요렇게 표 냈지만 이것까지
정리를 해서 요런 식으로 표현할 수 있게 된거죠 됐죠
그래서 여러분들이 물론 이런 과정을 거쳐서 직선의 방정식을 구해야
되겠지만 다음부턴 간단하게 와 있는 그렇죠
예 우리가 한 점은 이미 알고 있기 때문에 결국 와인은
기울기의 x - x 좌표
그다음 플라 스와 이 좌표 런 식으로 한 방에 직선의 방정식을 구해낼 수
있어야 된다는 겁니다
그쵸 ok 자 그럼 바 여기에서 우리가 정리 해서 표현해 본 요런 골에
대한 특징을 또 보도록 할까요
요런 이제 뭐가 되냐 하면 잘 가라
물론 우리한테 주어진 점은 1 콤마 이지만
요렇게 정리를 하고 나면 어떻게 되냐면 요 잘 밥
우리가 1 콤마 있는 대추 요기 쯤으로 표현할 수가 있겠죠
그리고 기울기가 3이다 그랬을 때 우리가 이런 식으로 일어 어케 그저
가파른 직선 1 r 그릴 수가 있을 겁니다
근데 이렇게 정리를 해놓고 보니까 얘는 마치 와인은 사매의 x - 0 -
일로 표현한것 가 똑같죠
그럼 이 얘긴 뭔 얘기냐 얘는
2.0 콤마 - 이를 지나고
기울기가 3인 직성이 다 이렇게 생각할 수도 있다는 얘기에요
즉 0 콘 마일이 라는 점이 바로 여기에 있는 점이 구나
요점이 0 콤마 아 맞 일니라 - b 줘 영어 곳만 - 긴 점이
구나
이렇게 볼 수도 있다는 얘기지 그 즉 그래서 요런 형태가 어떤 형태 냐
면 바로 기울기와 바 이 직선이 y 축과 만나는 점을 지난다고 생각하고
9 1 직선의 방정식 입니다
근데 이 y 축과 만나는 요 첩 에 y 좌표를 우리가 뭐라고 분야 면 y
절편이 다 이렇게 보기 때문에
y 절편이 - 일이다 라는 얘기는 곧 아이 직선이 0 콤마 - 이를지
나는구나 이렇게 볼 수 있는거구요
결국 그 점을 이용해서 9 1 직선의 방정식 2 바로 요렇게 되는 거지
그래서 얘는 기울기와 y 절편을 로 구한 직선의 방정식 이다 라는 것도
여러분들시면 되겠어요
그래서 궁극적으로 하고 싶은 얘기는 뭐냐면 잘바
예를 들어 직선의 방정식은 와인은
mx 플러스 앤의 꼴로 주어지게 되는데 요 때 당연히 앱은 뭐가
되는거구요
기울기가 되는거구요 요때 애니 뭐야
바로 y 절편이 된다는 겁니다
y 절편이 뭐라고 직선이 y 축과 만나는 점의 y 좌표가 되는겁니다
따라서 과 예를 보면 우리가 쉽게 볼 수가 있어요
그저 얘를 보면 은 예를 들면 기울기가 얼마고
기울기가 - 295 그저 y 절편이 일이다
이렇게 주어진 직선의 방정식은 와인은 그 3
기울기 - ex 절편 1 이렇게 쓰면 됩니다
이게 훨씬 더 간단하고 쉬운 형태 란 얘기지
x 다영 넣으면 y 가 1 나오는 거니까 x 좌표가 영 이라는 건 와
이 축과 의 교점 이구나 라는 걸 우리가 볼 수가 있는 거죠
이해가 되십니까 그래서 대개는 요러한 형태로 직선의 방정식을 표현하게
되는데
요러한 예 그 직선의 방정식 2 가장 뭐예요 표준적으로 우리가 쓰는
직선의 방정식 딱 이렇게 생각하시면 됩니다
누구와 누구 로 나타내 기울기와 y 절편을 로 나타내
물론 꼭 y 절편을 필요는 없어요 1점이 그냥 요러한 형태에서 애니
나타내는 게 바로 직성이 y 축과 만나는 점의 y 좌표 즉 y 절편이
달하는 것만 여러분이 알고 계시면 됩니다
됐죠 ok 자 그럼 바
이제 2점이 주어진 경우 2정 x1 y1 그 다음에 x2 y2 를 지나는
직선의 방정식
예 대해서 한번 생각을 해 봅시다
아까는 다르죠 음 아까는 1점과 기울기가 주어져 썼는데 지금은 2점이
주어진 게 있습니다
자 그렇지만 바 결국은 이 직선 위의 두 점이 있다 란 얘기잖아요
x1 y1 이라는 점과 x2 y2 라는 점이 있다는 얘긴데
이 때도 마찬가지입니다 우리는 요기에 한적 이미 의 접을 x 콤마 y 로
잡으면 되구요
우리의 최종적인 목적은 2 x 와 y 에 관계식을 구하면 됩니다
그런데 아까 우리가 만약에 한 청 1 접을 주어진 1점을 x1 y1
이라고 보고요
기울기 애미 있을 때에 직선의 방정식은 쉽게 구하는 방법을 배워 짠 아
그럼 우리는 여기서 필요한 5 입어야
기울기 만 구하면 된다 이와 기울기 m 이라는 놈은 자 잘바
2점이 주어졌지만 아 근데 아까도 말씀드렸지만 직선의 기울기 라는 것은
직선이 갖는 고유한 성질 특징이기 때문에 어떤 두 점을 갖고 구해도
똑같은 값이 나오게 된다 라는 거죠 그래서 우리는 간단하게 그냥 주어진
점이 두 개가 있으니까 이 두 점을 이용해서 기울기를 구해 버리면 됩니다
그리고 1점 물 x1 y1 으로 보면 되는 거죠 그러면 상당히 간단합니다
아까 봐 우리는 와인은 ml x - x1 플라스 y 원으로 직선의
방정식을 구할 수 있다고 했지
그러면 지금 이 상황에서는 우리는 앱을 그냥 x2 - x1 분 의 y2
- y1
그다음 x - x 원 플러스 y1 으로만 바꿔주시면 된다는 겁니다 됐죠
이게 바로 보냐 하면 2점이 주어져 있을 때에 직선의 방정식의 됩니다
그럼 여러분이 알아야 될 거 뭐냐 전부 개가 주어져 있을 때에는 누구부터
보았다
무조건 그저 예 기울기 부터 구해라
기울기 부터 구해라 요것만 보시면 되요 그러면 한 점과 직선의 기울기
로부터 우리가 직선의 방정식을 찾아낼 수 있게 됩니다
자 물론 그 한 점을 굳이 x1 y1 으로 볼 필요는 없습니다
2 x1 y1 대신 x2 y2 를 나머지 한 점이 다 그 저가 기울기는
m 이고 1점이 x2 y2 옆 따 이렇게 해서 직선의 방정식을 구해도
아무 상관이 없어요 똑같은 식의 나오게 됩니다
당연히 그렇겠지 그래서 우리가 이 책 썬의 방정식을 와인은 x2 - x1
분해 외 y2 - y1 즉 기울기 그다음 x - 엑스투 브라스와 인 투
로 써도 이 둘은 쌤 셈이다
똑같은 놈이 된다는 겁니다 오케이
음 그래서 이렇게 2점이 주어 졌을때 직선의 방정식은
그 두 점으로부터 키울 길을 먼저 구하고 그 다음에 애가 됐든 예가 됐든
2점 중에 아무나 창의가 좋아하는 1점을 선택해서 그 접을 지나가는
직선의 방정식 을 구하면 된다
이렇게 생각하시면 됩니다 됐죠 오케이
이번 시간에 우리 그 아참 까 예를 하나 볼까요 얘도 기원 보게 될
그럼 바라 우리가 뭐 1 콤마 삶과
- 2 콤마 이를 지나가는 직선의 방정식을 구하세요
라고 문제가 나왔다면 긴게 n 부터 구하시면 됩니다 그러면 - 2 - 1
분해
1 - 3 이렇게 되면 되겠죠 그럼 얘는 어떻게 된건 2 - 3 풀의 -
요렇게 되는거구요 결과적으론 기울기는 3분의 2가 됩니다
그리고 2개의 중에 아무거나 하나 마음에 드는 놈을 에 그냥 한 적으로
보면 된다고 했죠 우린 그냥 1 콤마 3을 본다면 우리가 구하는 직선의
방정식은
기울기의 x - 1+3 요렇게 쓸 수가 있습니다
다르게 표현하면 와인은 3분의 2 x 그 다음 - 3분의 2 의 3분의
9 가 더해진 거니까 플러스 3분의 7 요렇게 우리가 쓸 수가 있게
된거죠
땅 속에는 기울기가 3분의 이고 y 절편이 3분의 7인 직성이 다 이렇게
말을 할 수가 있게 된거죠 됐죠
ok 자 이번 시간에 우리가 한 점과 기울기가 주어 졌을때 의 직선의
방정식 2
그리고 2점이 주어 졌을때 직선의 방정식을 구하는 방법에 대해서
알아봤습니다
여러분들 이 두 가지만 알고 있으면 앞으로 나오게 된 모든 직선을 다
해결할 수 있어요
걱정하지마시고 요 두가지 방법
사실은 한 가지입니다 왜냐하면 부 점이 주어져 가짜 우리는 기울기 부터
구할 거기 때문에
그지 그래서 고 것만 정확히 알고 계시면 직선의 방정식을 구하는 데
에서는 아무런 문제가 발생하지 않게 될겁니다
알겠죠