수학중독 원의 접선의 방정식 > 중학교수학

 

이번 시간에는 원외 접선의 방정식 에 대해서 알아보겠습니다
자 지난 시간에 우리가 그 원인이 직성이 접한다.는 것은 어떤 건지 배웠죠
그저
원 이렇게 있을 때 접한다.는 것은 원과 직선의 교점 이 정확히 하나가
존재한다. 라는 걸 얘기하고 요
이때 이 직선을 이 위원회의 접하는 선이다 이래서 접선 이라고 부릅니다
그 점에서 접한다.는 건 무슨 의미냐 하면 원과 직선의 교점을 이미 단
하나 존재한다. 라는 의미가 됩니다
자 그렇다면 우리가 지난 시간에 배운 바에 의하면 결국 원의 방정식과
직선의 방정식을 열리 판 x 에 대한 이차방정식 판별 씩 키가 있고
0이다 나는걸 떠 올리셔야 되구요
또는 이 경우에 원의 중심에서 부터 직선 까지 의 거리가 반지름 r 과
똑같다 라는 요 두가지 조건
아 두 가지 조건이 동시에 필요한 건 아니고요 뭐 요 조건으로 보시던가
혹은 아래에 있는 조건으로 보시던가 둘중에 하나만 보시면 됩니다
그리고 또하나 여러분들이 알아야 될게 우리 중학교 때 다 배워서 알고
있겠지만 이 원의 중심에서 접선의 내리 이 수선의 발이 곳 이적 점
접하는 점이 되는거구요
결국 요놈 과 요 몸이 직각이 된다 즉 중심과 접점을 지나가는 요 직선이
적성과 수직이 된다 라는 것 정도는 여러분이 알고 계셔야 됩니다
됐죠 자 그러면 우리가 아냐 3가지 정도의 대해서 이 원의 접선의
방정식을 구하는 방법을 알아보도록 하겠습니다
자 첫번째 가 뭐냐면 첫번째
접점이 주어지는 경우입니다
적정 이 주어지는 경우 이렇게 보시면 되겠네요
먼저 우리가 쉽게 보기 위해서
원의 방정식 2 x 의 제곱 프라스 와인 제고 분이 꼴 r 제곱으로
주어질 때 부터 보도록 하겠습니다
즉 원의 중심이 원점 인 경우 부터 보게 딴 얘기 입니다
자 그럼 바라 얘가 이런 식으로 중심이 원점 인 요런 원이 하나가 생길
테고요
이 위에 젊 x1 콤마 y1 이 주어졌다 라고 한번 생각을 해 봅시다
x1 y 모든 이 두 적 아 이 점은 바로 이 원 위에 있는 저 되겠죠
그러면 이 점에서의 접선의 방정식 써는 그림이 어떻게 되냐면 대충
이런식으로 요렇게 나오겠네요 그저
그리고 우리가 꼭 확인해야 될 건 뭐냐면 이 중심 원점으로 부터 이 적성
까지 의 거리가 반지름 과 똑같다 라는 걸 알 수가 있습니다
그저 게다가 이 원 점 과 접점을 연결한 요 직선이 2 접 썽 과 수직이
됨을 또 우리가 알고 있는 거죠 자 그러면 바울이 가 쉽게 구할 수가
있게 보세요
요 빨간 5을 연장한 직선을 한번 생각을 해 봅시다 요런 직선이 있다
라고 했을 때 이 직선의 기울기가 얼마냐 라는 거야
요 직선의 기울기는 당연히 x 증가량 불의와 이 증가량 이기 때문에 x1
- 0
즉 요 두 점을 갖고 기울기를 구해보면 y1 - 0 해서 x1 분 의 y
원인이 되는 걸 볼 수가 있죠
그렇다면 바 우리가 배워서 알고 있잖아
이놈과 수직인 2 접선의 기울기 는 당연히 - y1 분 의 x1 이
되어야 합니다
맞죠 왜 이 2를 곱해서 - 1위 나와야 되거든요
그 직 짝 따라서 파 2 위의 점 x1 y1 이 주어진 상태에서 이
점에서의 접선의 방정식 음 한 점이 나왔고 기울기 까지 나왔기 때문에
우리는 한방에 구해낼 수가 있습니다
와인은 기울기 - y1 분 의 x1 x - x1 플라 스와 임원 이렇게
된거죠
이름이 바로 우리가 구하는 접선의 방정식 에 됩니다
자 그런데 보기가 불편하지 않아 좋지 않지 그래서 양변에 우리가 y1 을
곱해 주면 y1 y 는 자 전개 합시다 - x1 x
그다음 플러스 x 워렌 최고 프랑스와 2월에 제곱 됩니다
와 잉어를 곱하면 요놈 만 없어지고 요렇게 요렇게 전개한 거고요
당연히 여기에 도와 이원익 5패 지기 때문에 y1 제곱이 된거죠
자 그럼 이걸 정리하면 잘바 요놈을 정리하면
x1 x 플라스 y1 y 는 x 원 의 제고 플라 스와 2월의 제곱 인데
우리가 e x1 y1 2
이원 위에 점이라고 했으므로 당연히 이 x1 y1 을 x y 에 각각
대입하면 져 원의 방정식을 만족하게 되겠죠 즉 등식이 성립한다. 는 뜻이
됩니다
따라서 x1 제곱 프랑스 y1 제곱은 r 제곱 이 되기 때문에
요 부분이 바로 알 직업이 되는 거죠
결국 우리가 얻을 수 있는 접선의 방정식 은 x1 x 플라스 y1 y 는
이꼴 과할 제곱이 됩니다
요놈을 여러분들이 기억하고 계셔야 되요 러
요게 뭐냐면 중심이 원점 이고 반지름이 알로 주어지는 원 위의 점 x1
왕 위원회에서 의 접선의 방정식 2 됩니다
ok 이 무지하게 중요합니다 이것 꼭 기억하셔야 되요 꼭 알고 계셔야
됩니다
이거 하나 알면 풀리는 큰 반 풀리는 문제를 이걸 몰라서 막 오븐 10분
헤매는 학생들을 너무
많이 봤습니다 알겠죠 즐겁고 기억하도록 하세요 됐죠 자 그럼 바라나
요놈을 일반적인 경우로 한번 확장을 해보자 라는 거야
일반적인 경우 라는건 결국 x - a 의 제곱 플러스 y - b 의 제곱
이 꿀 r 제곱 이라는 요원 위의 점 x1 왕이 원해서 의 적선 에
방정식은 어떻게 구할 거냐 라는 거죠 그럼 하라
얘가 원이 이렇게 있는 거야 그렇죠 그리고 여기 중심 있어 이 중심의
좌표가 지금 에이콘 마피아 그리고 u 위에 원 위의 점 x1 y1 이
있을 때
여기서 에 적선 에 방정식 요놈은 또 어떻게 구할 거야 라는 거야
다르지 않습니다 지금 한 거랑 똑같아요
그럼 바라 u 빨간거 이 빨간 2정 중심과 x1 y1 을 연결하는 이
빨간 직선의 기울기는
x1 - af y1 - 비가 될 거구요
따라서 이 녹색 즉석 즉 접선의 기울기 는 - y1 - b 분의 x1 -
a 가 될 거다 라는 걸 알 수가 있죠
왜 이 둘이 수직 이고 각각의 기울기를 곱해서 - 일이 나와야 되기
때문에 그런 끝났네
기울기 나왔고 1 좀 나왔으면 와인은 - y1 - b 분해 의 x1 -
a x - x1 프라 스와 이인권
요렇게 우리가 쓸 수가 있다라는 겁니다 자 별거 업적
그러면 우리가 두 번째 기울기가 주어지는 경우에 대해서 알아보도록
하겠습니다
이것도 두번째 기울기가 주어지는 경우 9
우리가 첫번째 더 제목을 써 썼나요 예 안 썼으면 여러분들은 그냥 알아서
쓰도록 하세요
자 기울기가 좋아지는 경우도 우리가 원점에 중심이 있는 경우 부터
알아보도록 하죠
이렇게 되는 겁니다 아 그 다음에 y 아 기울기가 됩니다
그저께 니 애미다 이렇게 그쵸
기울기는 애미다 이렇게 주어지는 경우를 한번 생각해보도록 하죠
자 그럼 아 우리가 기울기가 m 인 직선의 방정식은 요 와인은 mx
플라스 애니 다 이렇게 놓을 수가 있겠죠
물론 meo 기울기가 존재하지 않고 y 축에 평행한 몸에 접선 은요 쉽게
구애를 수 있습니다 뭐 그런건 여러분들이 알아서 보시면 되고요
기울기가 애미 이렇게 주어진 경우에 우리는 애니 뭐냐 라고 만 게 아 m
만 구애 내면 되는 거죠 그럼 바 이 원의 중심은 0 콤마 0 이구요
이 중심에서 이직 선까지 의 거리가 반지름 r 과 똑같아 야만 얘가 뭐가
된 거야
바로 이 원의 접선 이 된거죠 따라서 우리는 0 콤마 0에서 전원
정리하면 mx - y 플러스 애니 꼰 영이라는 직성이 됩니다
요 두 놈 사이의 거리 길을 먼저 구하는 겁니다
이 먼저 거리 뒤 를 구해보면 루트에 m 제곱 x 계수의 제고 브라스 y
계수 의 제곱은 일이죠
분해 2 절대 깝 바 영영을 x y 에 각각 대입하면 남는 놈은 앤 밖에
안 남 따라 라는걸 알 수가 있습니다
됐죠 따라서 요놈
2 반지름 r 과 같을 때가 바로 이 직선이 인권의 접할 때 달하는 것
볼 수가 있죠
자 우리가 지금 궁금한 건 애니 뭐냐 라는 검으로 그저 우리는 얘 내
2절 대가 밴스 가 절대 카페는 r 곱하기 루트 의 m 제곱 플러스 일로
쓸 수가 있구요
결과적으로 내는 플라스틱 - 절대값이 벗겨져 쓰니까 아래의 노트에 n 제
고파스 일로 쓸 수가 있습니다
자 따라서 요렇게 중심이 원점 이고 반지름의 길이 까 아린 원에 접하는
길기 애 민 접선의 방정식 은 어떻게 쓸 수가 있냐면 정리를 하면 이렇게
되겠어요
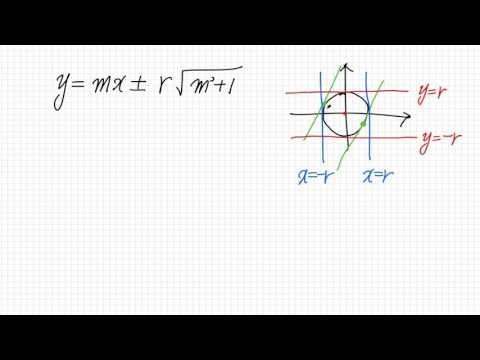
와인은 mx 플렉스 - r
루트 m 제곱 플러스 일이다
요렇게 쓸 수가 있게 되겠네요 그저
꼭 선생님 왜 두개가 나오나요 이렇게 말씀들 하시는데
파악
우리가 중심이 원 점 인원을 요렇게 그렸을 때 만약에 목 기울기가 2인
적선을 구하라 그러면 기울기가 이라면 여기서 하나가 나오구요
또 어디서 하나가 나와 여기서 1 두 개가 나오게 됩니다 즉 아까처럼
접점이 많이 접점이 여기다 라고 주어졌다면
그때 이 접선 접점에서 에 접속 는 요거 하나 밖에 없지만 지금처럼
기울기가 주어진 경우에 원에 접하는 적선 은 두 개가 되는 걸 볼 수가
있어요
배 점 박 심지어 기울기가 0인 놈 부여
이렇게 이렇게 2개가 되는 것을 볼 수가 있죠 그래서 예를 들고 기울기가
0이다 그러면요
그냥 쉽게 구할 수가 있어요 중심에서 부터 반지름 만큼 올라간 즉 와인은
이꼴 알과 와인이 꼴 - 알이 뭐가 된 거야
바로 첩 썬의 방정식이 된겁니다 그래서 아까 쉬우니까 선생님이 여러분들이
직접 해보세요 라고 말했던 겁니다
그럼 당연히 봐 y 축에 평행한 적성 이 이걸 거 아니고 이렇게
그래서 이놈도 똑같이 우리가 x 는 - r 과 x 날이다 라는 걸 볼
수가 있습니다
즉 중심에서 부터 알만큼 도 하고 중심 액수 좌표에서 알만큼 뺑 뭐가
바로 보아야 접선이 되는겁니다 이렇듯 우리는 기울기가 주어진 상태에서는
에 그 기울기 에 해당하는 접선 은 2개씩 나온다는 것 꼭 기억하시기
바래요
자 지금은 선생님이 중심에서 부터 에 뭐야 그 접점 까지 의 거리 같죠
접 선까지 의 거의 거리가 반지름 r 과 똑같다 를 이용했는데
우린 그 양파 x 제곱 플라 스와 이 세법은 알제 법과 와인은 mx
플러스 애는
2개를 열리 패서 x 에 대한 2차 방정식을 만든 후에 급한 별식 익고
영의 다 를 이용하셔도 됩니다
즉 x 의 제곱 플러스 자와 이 대신에 요놈을 대입하면
mx 플라스 nl 제고 분이 꼴 아 이제 곡이죠
요것 전개하게 되면 m 제고 플러스 이래 x 의 제곱 이구요 플라스 em
nx 플러스 앵 제곱 - r 제곱 은 이꼴 0이 됩니다
요놈의 판 병씩 을 보면요 우리가 4분의 뒤를 보면 되겠네요 그저 4분의
d 는 b 다시 의 제곱 즉 m 제곱의 n 제곱 이렇게 잖아요
- ac
니까 m 제곱 플러스 1 그 다음에 n 제고 - r 제곱 요놈이 꼴 0
되는걸 9 하시면 되겠죠
실제로 예를 한번 해보면 요 - m 제곱 n 제곱 플러스 m 제곱 r
제고
그다음 - n 제고 플라스 r 제곱 예 맞죠
요렇게 있고 0 여기 된걸 볼 수가 있습니다
자 그러면 우리는 n 제곱 요 요 두개는 없어지네요
그럼 남는 것은 n 제곱 은 그저 r 제고
요거 두개 내요 r 제곱 으로 묶어 주면 결국 m 제곱 플러스 일이구요
따라서 애니라는 놈은 플라스크 - 아래의 루트 m 제고 플러스 일이 된
것을 볼 수가 있습니다
자 따라서 우리가 첫번째 방법 이었죠 툴을 열리 패서 판별 시기 꼴 0
이다 라는 거 로부터 n 값을 구해야 될 수도 있습니다
되 초 자 그럼 이 경우도 마찬가지입니다
예를 들어 중심 잊지않고 아 중심이 원점에 잊지 않고 이렇게 일반적으로
에이코 마비가 중심이며 반지름이 r 제곱 이놈의
기울기가 이꼴 내민 적선 은 어떻게 구할 거냐 똑같죠
결국 와인은 dmx 플러스 애니 될거구요
중심이 a 콤마 피니까 결국 2a 콤마 비로부터 이 직선 까지 의 거리
한번 구해 볼까요
루트 m 제고 플러스 1 분해의 자 절대 까
누가 됩니까 갖다 놓으면 ma - b 플러스 행이 됩니다
요놈이 반지름 r 과 똑같단 로부터 우리가 구해낼 수가 있겠죠
따라서 애니라는 검은 어떻게 구해야 면 자 ma - b 플러스 애니라는
놈은 r 루트 m 제고 플러스 일이기 때문에
결과 플러스 마이너스 가 빠졌네요 왜냐하면 여기 절대 값이 벗겨 줬으니까
따라서 애니라는 몸은 여기서 열로 는 겁니다
애니 라는 놈은 그저 b - ma 플러스 마이너스 아래의 노트 m 제고
플러스 일이다
요렇게 구애 내실 수가 있습니다 이게 상당히 복잡해 보이는데
어차피 기울기는 숫자로 주어질 거구요 수 짜고 중심의 좌표 도수 짜기
때문에 어렵지 않게 우리가 목을 계산해 낼 수 있다는 것을 알 수가
있어요 그렇죠 뭐 여러분들이 예를 만들어서 하나씩 계산해보면 아 선생
말이 이 얘기
나아가 그걸 알 수가 있을 겁니다 그렇죠
ok 자 그 다음 세 번째는 뭐냐면
곡산 밖의 한 점 이브가 원밖에 안 점이죠 곡선이 라 그렇지만 이 우리가
원 이라고 합시다
원밖에 1점
한 점이 주어진 경우입니다
요거는 어떻게 하는지 방법만 여러분들한테 말씀을 드릴게요
예를 들어 이건 뭐 원 점도 필요없습니다 자파 원 외에 중심이 a 콤마
비구 요 요 바깥에 x1 y1 이라는 점이 있다고 합시다 그러면 이 x1
y1 을 치 나가면서 원에 접하는 접선의 방정식을 구하세요 라는 문제가
나왔을 때 우리는 결국 요런 그저 요런 접선의 방정식을 구해라 라는 거죠
자 그럼 파 2
접수는 요 기 우리만 모르고 한 점이 주어진 상태이기 때문에
와인의 기울기를 그냥 니 애미다 이렇게 보면 x - x1 프라스 y1
요로케 보면 됩니다 그런 팔아 결국 또 원의 중심에 이코마 피해서 부터
이 직선 까지 의 거리가 반지름 r 과 똑같다고 볼 터 우리가 문제를
풀어낼 수가 있는 거죠 그래서 이걸 정리하면 앱 x - my - mx
1ts 왕이 원은 이꼴 영이 되구요
중심의 좌표는 외 2건 마비 니까
2 에이콘 마비 로부터 여기까지의 거리 이것까지 만 한 번 해볼까요
노트에 m 제곱 플러스 1
분해의 절대 깝 ma - b - mx 원플러스원 인권 이 반지름 r 과
똑같다 에서 n 값을 구해 내실 수가 있다라는 얘기입니다
요거 m 값을 구해 되면요 앤 까이끼 m 에 대한 2차 방정식이 됩니다
요거 이렇게 넘긴 다음에 양변을 제 곱하면
그럼 m 값이 두 개가 나올 텐데 왜 두개가 나오냐 하면 요
원의 바깥에 1점이 주어졌을 때는 접선을 이렇게 그릴 수도 있지만 어떻게
그럴 수 도 있어요
요렇게 그럴 수도 있죠 그저 그래서 이렇게 접선 이 두가지가 나오게
됩니다
그래서 n 값이 두 개가 되는걸 볼 수가 있어요
돼 점 요건 여러분이 직접 한번 해보시기 바랍니다 안녕
여러분들의 갖추고 있는 어떤 교재를 보더라도 예와 관련 되기에 제가
나와있을 거에요
오케 작은방
결국 원의 접선의 방정식을 구할 때 우리가 가장 손쉽게 써먹을 수 있는
것은 바로 원의 중심에서 부터 접 선까지 의 거리가 반지름 과 똑같다는
거구요
두번째 이원구 원의 중심과 접점을 연결한 요 직선과 접사는 서로 수직 즉
두 직선의 기울기를 곱하면 - 일이 된다 라는 걸 이용했다 그걸 꼭
기억해 주시기 바랍니다
알겠죠 여러분들 공식처럼 왜 울려고 하는 것은
익숙해진 다음부터 해요 그래서 여러분들 꼭 기억해야 되겠지만 일단
문제들을 풀면서 선생님 있었던 방법들을 적용하다 보면 어느 순간 나도
모르게 공식을 암기하고 있는 자신을 발견하게 될 겁니다
알겠죠