수학중독 | 인수분해 3
본문
※ 영상을 선명하게 보기 안내
- 유튜브 영상에서 오른쪽하단에 톱니바퀴를 클릭합니다.
- 팝업목록에서 "품질" 선택하세요.
- 원하는 해상도를 선택해주세요.
※ 모바일에서 Wifi가 아니라면 데이타가 소진될 수 있으니 주의바랍니다.
수학중독님의 중학교수학강의 청각장애인을 위한 자막
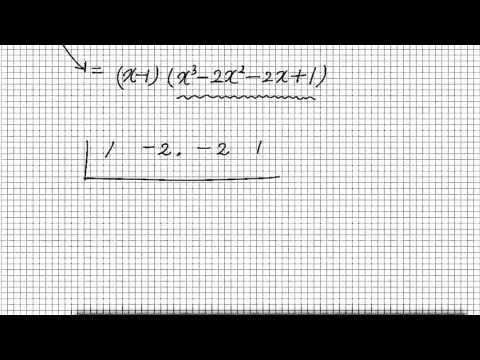
인수 분 의 세번째 시간입니다 이번 시간에는 우리 복잡한 식의 인수분해
부터 시작을 할 텐데요
이 복잡한 시기라는 것은 말 그대로
문자가 되게 여러개 등장하는데 뭐 엄청나게 그냥 눈에 보기에도 복잡해
보이는 식을 1 수분의 하라
뭐 이런 얘기에요 예를 들자면 이런거 조 x 의 세제곱 파라스 x 제곱의
gets xg 의 제곱 그다음 - y 에 세제곱 - y 잭 없지
그저 그 다음 - yg 에 제곱 요렇게 요 식을 인수분해 하여라
나하고 나왔다고 칩시다 아 그냥 보기에도 대단히 복잡해 보이고요
게다가 x 만 나온것도 아니고 x y 만 나온것도 아니고 그 액수와
의지까지 등장을 해서 이걸 도대체 뭘 공통 인수로 묶어야 되는건지 뭘
어떻게 해야 되는 거지 이건 뭐 공식도 없고 보이차 식을 쓰면 이 그것도
아닌거 같고 상당히 어렵다고 합니다
자 이럴때 룰이 있어요 이 복잡한 식의 인수분해 는 그저 에 차 쑤가
가장 낮은 몹
가장 낮은 놈으로 낮은 몸에 대해서
내림차순으로 정리하라
내림차순 전기 애가 이러한 복잡한 식을 인수 분해 하는 가장 좋은
방법입니다
그럼 착수가 가장 낮은 놈은 뭐냐면 우리가 찾 쑤가 높다 낮다 를
결정하는 건 소위 말해서 최고 창입니다
그럼 바 예를 들어 x 같은 경우에는 가장 높은 차수가 지금 x 의
세제곱 이 등장을 했네요
맞죠 그다음 y 같은 경우에도 가장 높은 차수는 y 에 세제곱 입니다
그런데 지를 보면은 가장 높은 차수가 지혜 제곱 이래요
맞죠 에 혹은 여기도 제국 그래서 우리가
아이 중에 차수가 가장 낮은 먹은 누구냐 x 도 아니고 y 도 아니고
바로 지구 나라는 것을 알 수가 있는 겁니다
따라서 이런 경우에는 우리가 지에 대한 내림차순으로 정리를 해주는 거죠
즉 지젝 5부터 써 주는 겁니다
한번에 묶으면서 가볼게요 그러면 요렇게 되는 거죠
대처 그럼 요 두 놈이 해결이 됐구요 그 다음에 g 가 들어가 있는 놈
두 놈 을 묶어주시면 x 제곱 빼기 y 제곱 에 쥐 가 됩니다
마초 그다음 나머지 요 두 놈 해결이 됐으니까 나머지 보시면 x 의
세제곱 빨기 y 세제곱 요렇게 된거예요
그렇죠 자 그럼 마 얘네들을 다시 우리가 정리를 해주면 보세요 여러분 x
- y
그다음 x 플러스 y 합 차 공식입니다
그다음 곱하기 지가 되는거구요 요놈은 우리가 인수 분 의 공식에 의해서
x 102 와 이에 x 제곱 플라스 xy 플라스 y 제곱으로 인수 분해
가 됩니다
자 그러고 났더니 똑같은 놈들이 보이더라 합니다
인수 분해 의 가장 기본이 져 공통 인수로 묶어 내라
따라서 x - y 로 묶어 주시면 요놈이
지게 제곱 그다음 프라스 x 프라스 y 의 g
그다음 플러스 놓아 되 거야 x 의 제곱 브라스 xy 플라스 y 제곱 이
되더라 라는 것을 볼 수가 있게 되는 겁니다
이런 다시 정리하면 우리가 x - y 에 자기 보세요
세제곱 y 에 제 9 그다음 지젝 5+
xi 그 남 요거 전개하면 yg 플러스 gx 가 되는 것을 볼 수가
있습니다
즉 이렇게 복잡한 식의 인수분해 를 요구할 경우에는 차수가 가장 낮은
놈에 대해서 내림차순으로 정리 해라
이걸 꼭 기억하셔야 됩니다 알겠죠
자 하나 더 해볼까요 예를 들면 이런 적 있어
x 의 y 제곱 플러스 d 제곱
그 다음에 프랑스 y 의 x 제곱 플러스 지젝 5
그쵸 그 다음에 플라스 치의 x 제고 프라스 y 제곱 그 다음에 8
sexy 지가 이렇게 또 시기 주어졌다 라고 생각을 해보자 이 거야 자
이거 근데 가만보면 요
이 최고 참을 봤더니 스포 x 도 최고참 은 2차 y 도 최우창 은 2차
지도 최 부차 흔히 차입을 볼 수가 있어요
꼭 5 소지금 이럴땐 어떻게 하죠 찾 쑤가 가장 낮은 몸에 대해서
정리하라 그랬는데 차수가 다 똑같잖아
아 그럴 때 누굴 선택해도 관계 없습니다 여러분이 좋아하는 놈 그 놈 을
선택해서 개에 대한 내린 찾으로 정리해 주시면 되요
우리는 x 를 한번 선택해 볼까요 그럼 파 x 제곱 이 나오는 놈이 여기
하고 여기있네요 그 정
따라서 우리는 y 플러스 g 로 묶어 준 다음에 x 제 곱해 주시면
되고요
그다음 x 가 등장하는 놈은 여기 x 로 묶여진 몸이 있고요 그 다음에
여기 또 x 가 등장합니다 따라서 얘는 y 제곱 플러스 요렇게 써볼까요
이 와이즈 플러스 지 제곱의 x 가 되고요
그다음 x 가 등장하지 않는 즉 x 에 대한 식으로 봤을 때 3 수에
해당하는 거미 yg 의 제곱과 지와 이제 법이니까
우리가 예를 yg 로 묶어 버리면 y 플라스틱 아 된걸 볼 수가 있습니다
됐죠 어 그런 봐라 얘가 뭐가 되냐 하면 결국은 또 y 플러스 치 전체의
제곱이 되는거니까
결국은 누가 또 보여요 y 플러스 g 와 2+ g
yv yg 의 yg 그제 예 뭐 이제 가수 되고 싶고 그런 생각이 들지만
여러분 안되는거 알고 있죠 그저 자 그럼 보세요
y 플러스 g 요렇게 되는건데 얘 로 묶어 버리면 x 의 제곱 플러스
y 플라스틱 아 하나가 그대로 남고 요 플러스 yh 이렇게 된걸 볼 수가
있습니다
따라서 이 롬은 y 플러스 지에 자의 겉에 인수분해 되요
이제 뭐 눈에 보이죠 x 플러스 y 와 x 플러스 g
요렇게 깔끔하게 인수 분해 가 되는 것을 볼 수가 있습니다
됐죠 그래서 요런 식의 문제들이 상당히 또 많이 출제가 됩니다
사실 수 학원이 시험 범위 에 속하면 이런 문제들이 나오는데
수 학원이 시험 범위에 속하지 않으면 사실 이 수분의 에서는 그다지
어렵게 인수 불이 하는게 나오잖아요
그 정 일단 여러분들이 수 학원을 공부하고 있는 중이라면 이런거에 좀
신경을 쓰셔야 되고요
여러분이 바로 수능을 앞두고 있다라고 생각 된다면 그 정
요런 군은 좀 신경을 거둬 될까 라고 말하면 훌륭한 선생니겠죠 그죠
예 어쨌든 열심히 하세요 때 점 자 그 다음
그 다음에 이제 우리가 조립 째 법 을 이용하는 고차 식의 인수분해 가
있어요
조립 째 법 을 이용하는 곳 차시 게임 수분의
자 사실 시험 애 여러분이 고 3 이라면 시험에 또 많이 등장하는 놈이
바로 요놈 입니다
요놈은 정말 잘 알고 있어야 되요 그점
예를 들면 봐 우리가 그 모르겠어 냐 면
f 에 a 가 이꼴 0 이라면 어
이것은 x - a 에 qx 꼴로 fx 를 표현할 수 있다 라는 거잖아 즉
fa 가 영 이란 얘기는
f x 가 x - 2로 나누어 떨어진다는 얘기 구요
그렇다면 이 fx 라는 놈을
우리가 x - a 곱하기 크게 x 로 표현할 수 있다 즉 이때 fa 가
영 이라는 얘기는 그지
우리가 어떻게 쓸 수가 있냐면 x - a 가 에프엑스의 인수 이다 라는
겁니다
그저 인수 중 하나이다 난걸 얘기한 거지
따라서 3차 이상 의식이 나왔을 때는 요
2 조립 째 법을 이용해서 나머지가 0이 되게 만드는 a 부터 차 짜라
는 거야 그러면 x - a 를 우리가 묶어 낼 수가 있구요
그때의 몫을 다시 인수분해 해주면 된다는 뜻이 됩니다
무슨 말인지 하나도 모르겠죠 자 그럴땐 얘를 보면 됩니다
자박 시계 우리 4차 식 한번 볼까요
예를 들면 x 의 내재 고백 - 3x 의 세제곱 프라스
3 x - 1 예를 인수분해 해라 라는 문제가 나왔다 고칩시다
이해를 인수분해 하려고 봤더니 애가 4차 식인데
중간에 또 x 제 곱하면 없구요
이거 뭐 어떻게 예수 분해를 해야 될지 잘 모르겠더라 라는 얘기 입니다
그쵸 자 그럴 때 밥 1 - 3
그 다음에 빈 자리는 영어로 뱉거나 그랬습니다 ex 제법 이고요
3 - 1 이렇게 되는 거죠 자
이때 우리가 잘바 이름을
x - 에 2로 나누었을 때 나머지가 0이 되게 끔 만드는 게 우리의
목표 잖아
그치 그러면 이 자리에 바로 a 가 와야 되는데 그 a 가 얼마 하겠느냐
라는 거야
자 그럼 아 이 a 를 찾는 방법 중에 가장 쉬운 방법이 요원들을 싹다
더해서 0이 되는 지를 확인하는 겁니다
어 이거 싹다 더 했더니 일과 - 없어지고
- 3과 3의 없어지죠 그렇게 되면 여기 들어갈 놈이 이익이다 라는
거예요
이거 꼭 기억하세요 호킹 왜 일을 없다는건 개수 들의 합을 보겠다는
얘긴데
여기다 이를 로서 그러면 예가 녕 된단 얘기잖아
즉 x - 일이 뭐가 된단 아니야 x - 일로 애가 나누어 떨어진다는
얘기니까 그제 우리가 찾는 놈은 일이 된다는 거에요 그래서 기억하세요
이것들을 싹다 더해서 0이 되면 이 장인 일이 들어갔다
오케이 그럼 1 1 곱하기 일이니까
요거 두개 더하면 - 2 2 자 요렇게 두개 곱하면 - 2
요렇게 두개 더하면 - 익 자 이렇게 두개 곱하면 - 2 2
요렇게 두개 더하면 1 자 이렇게 두개 곱하면 얼마
1 그쵸 그래서 엄마 영어 요렇게 되는 겁니다 그러면 방
요놈은 우리가 어떻게 쓸 수가 있냐면 x - 일이라는 인수를 끄집어 낼
수가 있는 거지
그지 그다음 말아 요 럼 2x 의 세제곱 - 2x 의 제곱 빼기
ex 그다음 플라스크 1 이렇게 된겁니다 됐죠
그럼 밥 이제 우리는 예만 인숙은 회를 하면 되는데
3차시 기니까 근데 얘도 역시 조립 째 법을 이용해서 이수 분해를 할 수
있다는 거야
그럼 왕 요놈을 다시 인수분해 보면 이렇게 올려 볼까요
1 - 2 - 2 1
요게 생과 자 그러면 요 자긴 또 누가 들어 가겠냐 일어 거지
자 아까 서기 뭐라고 했냐면 이거 싹다 더해서 0이 되면 2장에
들어가는건 일이다 라고 했는데 지금은 싹다 더해 도영이 안됩니다
자 그런데 우리가 보는건 봐 어 이 또 재밌습니다
요기 홀수 번째 등장하는 요 놈들의 합과 그 다음에 짝수 번째 등장하는
요 놈들의 합을 한 번 보자 2가
그러면 홀수 번째 들에 합이 얼마냐 하면 - 일이죠
게다가 짝수 번째 들에 합이 얼마냐 하면 - 일이었고 둘이 똑같은 아이
거지
즉 홀 쑤 번째에 합과 짝수 번째 것들의 합이 똑같으면 이 자리에는 -
일이 들어갑니다
이 됩니까 자 그럼 진짜 경우 가볼까
이런 그대로 내려 옵니다 요렇게 두개 곱하면 - 일이고요
둘을 더하면 - 3 입니다
자 요렇게 2를 곱하면 3 이고요 2를 더하면 일이죠
요렇게 2를 곱하면 - 일이고요 둘을 더하면 0
요렇게 된걸 볼 수가 있어요 끝났네 그럼 하라
얘는 결국 또 얘는 어떻게 우리가 쓸 수가 있냐면 x - 1
그다음 x 플러스 2 빚어 - 일이라는 몸은 - 이르렀을 때 0 되는
거니까 x 파 스 1이 와야 됩니다
그 다음에 x 의 제곱 - 3x 파스 일입니다
채찍 자 이 놈은 더 이상 인수 분해가 되지 않는 형태인 걸 알 수가
있죠
따라서 우리가 찾는 정답은 바로 요놈이 된다 라는 걸 여러분셔야
됩니다
됐습니까 ok 자 만약에 요 자리가 또 다시 요 2차 시기 또다시 인수
분해 가 된다 라고 하더라도
걱정할 거 없단 말이야 우리는 이미 2차 식의 인수분해 를 어떻게 하는지
알고 있더라는 얘기죠
따라서 고차 식의 인수분해 가 등장할 때에는 으
일단 1차 함대를 계속 뽑아내는 거야
누굴 통해서 조립 재 법을 통해서 언제까지 남는 요놈이 2차 시기 될
때까지
그리고 그 2차 식 부터는 조립 째 법을 쓰는게 아니라 그냥 2차 식의
인수분해 를 해버리면 된다는 겁니다
그쵸 오케이 작은방
기왕 해보는 거 몇 개 더 해 봅시다 자 3x 의 세제곱 플러스 7 x
의 제곱 빼기 사를 인수 분해 해라 라고 나오면 어떻게 할거냐 라는 거지
그지 조립 쩝 해볼까요 3 7
자 x 항의 없죠 빈 자린 영어로 채우라고 분명히 말씀드렸습니다
요렇게 한 상태에서 이제 요 자리에 얼마가 들어갈지 1 찾아보자 이 거야
제일 먼저 해봐야 될 건 얘네 들의 합이 0 되는지를 봐야 되죠
근데 얘네들이 합이 0이 안된다 거야 그럼 두번째 해봐야 될 건 뭐냐면
바 홀수 번째 계수 들의 합과 그다음 짝 수 번째 갯수 레 합의 똑같은지
봐야되는데 어 홀수 번째 계수에 합 또 3
짝수 번째 개수의 합 또 3 이니까 이 자리엔 얼마 들어간다고 이 경우에
- 일이 들어간다 라고 방금전에 배웠습니다 그쵸
그럼 바 삼은 그대로 내려오고 요렇게 2 곱하면 - 3
요렇게 더하면 그럼 요렇게 2 곱하면 - 4
그다음 더하면 - 이렇게 2 곱하면 더하면 영어 딱 떨어지는 걸
볼 수가 있죠
따라서 요놈은 우리가 어떻게 쓸 수가 있냐면 x 프라스 일과 삶 x 제곱
플러스 ex 102
요렇게 쓸 수가 있습니다
자 그러면 2차 시기 나왔으니까 더 이상 조립 째 법은 하는게 아니죠
그럼 여기서 볼 거야 아 이 놈은 3 곱하기 1
여러분 2 곱하기 2 자 크로스 로 곱하면 여러분 유기 되고 여러분이 가
되는데 우리는 자 더해서 를 만들어야 되니까 - 가 여기 붙으면
되겠네요
그리고 곱해서 - 딱 되는데 그 즉 결과적으로 우리가 인수 분해 를
마치고 나면 얘는 x 파스 1
그 다음에 3 x - 2 그다음 x 파 스 2
요렇게 인수분해 가 되는 것을 알 수 있다라는 겁니다 되죠
그 사람들 기억해 제일 먼저 해야 될 것은 계수 둘의 합이 0 인지
확인해서 개 가 0이면
요 자리에는 일이 들어갑니다 두번째 만약에 합이 0니라 그러면 홀
쑤 번째 개수의 합과 짝수 번째 개수의 합이 똑같은 가보세요
그래서 개가 0 이며 아처 코스 번제와 짝수 번 자비 똑같으면 그러면요
자리에 들어가는건 - 일이다 라는 거 기억하시면 됩니다
그렇죠 자 하나도 해봅시다 하나만 더 끝낼게요 파
ex 의 세제곱 그 다음 - 3 x 의 제곱 빼기
11 x 파스 6을 인 수분이 하여라 라는 문제가 나왔다 고 치죠 그럼
하라
2 - 3 - 11
6 그 다음에 요기에 얼마가 들어갈지 찾아야 되는데
얘네들 싹다 더해도 용이한 됩니다
그 다음에 홀수 번째 꺽기 리의 합은
- 구요 짝수 번째 것끼리 합은 3 이네요
역시 같지 않습니다 아 여기서 또 우리가 포기 해야 되느냐
아니야
일과 - 일니며 이를 보전해 보시면 됩니다 도저한 그제 그럼 아
요즘 고대로 내려오고 요의 이는 더하면 1
이 일은 이 더하면 - 쿠 2 - 9 곱하면 - 18
5 더하면 - 12 영이 안되네요
도전 실패 입니다 반짝 그런 바
도전을 실패했을 경우에는
좌절하지 말고 요 자리를 고대로 - 2 로 바꿔주시면 됩니다
그럼 해볼까 2 자 곱하면 - 더하면 - 7 곱하면 1더하면 3
곱하면 - 유경이 거봐 내 말이 맞잖아
그저 따라서 이름은 잘 바 얘는 x 플러스 2
그 다음에 ex 의 제곱 빼기 7x 프라스
3 요렇게 됩니다 그다음 다시 2차 시기 나왔으니까 2일 3일
크로스로 곱하면 6 얼마야 일이죠 그러면 뭐 해 주면 돼
둘다 - 붙여주면 요렇게 요렇게 해서 정확히 - 치게 되네요
됐지 따라서 우리가 최종적으로 얻을 수 있는 인수 분의 는 결국 x 파
스 2
그다음 ex - 1 x - 3의 된다는 것을 볼 수가 있습니다
자 여러분도 아마 의 할 거야
무지 혼자 이렇고 - 이거 특히 그럼 뭐 그런 배 많이 봤지 그럼 뭐
하는 거야 지금
이러는데 선생이 얘기해 줄게요
다 더해서 0 대문 일이라 그랬죠 그다음 홀수 번째 꽃길이 와 짝수 번째
것끼리 합의 똑같으면 - 일이지
여기에서 거의 80프로 가 걸립니다
즉 여태까지 출제된 문제의 80% 는 일 아니면 - 일로 일단 조립 째
법을 나누어 떨어져요
오케이 근데 그게 아니면 니면 - 입니다
ok 그래서 요 두 놈니다 그러면 먼저 이 보전의 보시고 도전
실패하면 - 2 하시면 되요
여기서 19% 가 버립니다
그러면 이건 네 개를 합치면 99% 가 걸린다는 일이지 그지
그럼 나머지 1% 를 뭐냐 당연히 그 다음 도전 할 것은 3
혹은 - 312 됩니다 그런데 이런 경우에 문제는 거의 출제되지 않아요
얘가 등장 한다.고 하더라도 봐 여기서도 사실 x100 232 등장해 끝
응 근데 예가 나오기 전에 우리 누굴 찾아 x 파스 2부터 찾는 거지 즉
래에서 먼저 나온 다음에 예가 나온다 이라
그럼 만약에 그 1% 할 건 뭐냐
얘네들이 전부다 안나왔는데 3이나 - 암이나 그게 바로 1% 야 5기
그럼 여러분은 1% 때문에 뒤통수를 맞을 수 있다는 것이 그지
근데 그건 출 제자들은 내가 밖에 변태 아 왜 그렇게 출제를 해
그지 그러니까 그냥 뒤통수를 마저도 아쉬 변태 한테 당했다 이렇게
생각하는데
물론 수능에서는 절대로 3이나 - 3의 나온적이 없습니다
무조건 1 - 2 - 2 해서 해결되는 문제만 나왔어요
알겠죠 선생님만 믿고 일단 4개를 도전 해 보신 후에 안되면 그 다음
3이라 - 4
근데 이거 두개 도 안됐다 그럼 그냥 그 문제 벌여 왜 니네 말고도
당신 말고도 이것 때문에 고민하면서 시간에 버지는 애들이 전국의 수도
없이 널렸다 이봐
그럼 걔네들은 거기에 시간 버리라고 하고 여러분은 그 시간에 풀 수 있는
다른 문제를 풀면 되는 것이 그지 약삭빠르게 알겠어
오케이 됐죠 여기까지가 바로 조립 재법 이용한 고 천식 의 인수 분입니다
대처 여러분들 꼭 수많은 연습을 통해서 예 늘 얘기하는 거지만 몸이
기억하게 만드세요
알겠죠


댓글 0개
등록된 댓글이 없습니다.